Em geral, apenas enunciados de exercícios.
Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por gigante2010 » Qua Out 20, 2010 22:51
por gigante2010 » Qua Out 20, 2010 22:51
1.Gostaria de saber como racionalizar o seguinte caso >>
![\frac{3}{\sqrt[2]{3}-2} \frac{3}{\sqrt[2]{3}-2}](/latexrender/pictures/c9d6af1dc7c19f439531dc37188c2213.png)
2.Como simplificar esse Radical >>
![\sqrt[5]{64} \sqrt[5]{64}](/latexrender/pictures/4d396534f3dff06bb97e27de112259b5.png)
3.Como calcular >>
![\frac{10 \sqrt[2]{9}}{5\sqrt[2]{3}} \frac{10 \sqrt[2]{9}}{5\sqrt[2]{3}}](/latexrender/pictures/2d555d11a8844f00aebe2fe94acf40a8.png)
4. E este também >>
![\frac{\sqrt[2]{27}}{4\sqrt[3]{2}} \frac{\sqrt[2]{27}}{4\sqrt[3]{2}}](/latexrender/pictures/3daa69230b9b12671bd1439125ff805a.png)
PS.: Queria algumas dicas tb, se não for pedir muito, sobre quando cai uma dessa >>
![\sqrt[3]{-54} \sqrt[3]{-54}](/latexrender/pictures/80c97ad00ad0f51e1f323ee333b4e2a8.png)
<< como é a fatoração dela?
Tb queria saber se um absurdo desses é assunto de ensino fundamental >>

quando

<< não consigo resolver.
-
gigante2010
-
 por MarceloFantini » Qui Out 21, 2010 15:21
por MarceloFantini » Qui Out 21, 2010 15:21
O primeiro caso basta usar
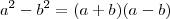
. O segundo, fatore 64. O terceiro, elimine a raíz do denominador. No quarto, fatore 27 e depois faça
![\sqrt[3]{2} \sqrt[3]{2}](/latexrender/pictures/9a132a1fa0d4f51451f00801ccbfe963.png)
virar

. Para o outro, lembre-se que
![\sqrt[3]{-a} = - \sqrt[3]{a} \sqrt[3]{-a} = - \sqrt[3]{a}](/latexrender/pictures/50d9645b37590b4d92e72b65dc742fa1.png)
e fatore. No último, lembre-se propriedades de expoentes, sinais e coloque

. Isso não é monstruosidade, isso é básico, e ajudaria muito se você visse como tal. Tudo que temos medo torna-se mais difícil.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por gigante2010 » Sex Out 22, 2010 01:53
por gigante2010 » Sex Out 22, 2010 01:53
Continuo sem entender. 'ff
-
gigante2010
-
 por MarceloFantini » Sex Out 22, 2010 07:57
por MarceloFantini » Sex Out 22, 2010 07:57
Você sabe o que é fatorar?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por gigante2010 » Sex Out 22, 2010 19:04
por gigante2010 » Sex Out 22, 2010 19:04
Eu sei fatorar, mas olha vey se não quiser responder não responde agora só não vem me subestimar ou me provocar, nun sei se deixei isso claro mas vou deixando: eu quero que RESOLVAM! e postem pra eu ver como faz. Principlamente essa fatoração quando o INDICE é 5, fatoro e depois agrupo os multiplos ele vando a 5?
-
gigante2010
-
 por MarceloFantini » Sex Out 22, 2010 22:56
por MarceloFantini » Sex Out 22, 2010 22:56
A sua resposta extremamente mal-educada responde a minha pergunta e muito mais. Eu não estava te subestimando, muito menos te provocando, eu fiz uma simples pergunta: se você sabia fatorar. Se você soubesse, quem sabe você percebesse que

e que ficaria
![\sqrt[5]{64} = \sqrt[5]{2^6} = \sqrt[5]{2^5} \sqrt[5]{2} = 2 \sqrt[5]{2} \sqrt[5]{64} = \sqrt[5]{2^6} = \sqrt[5]{2^5} \sqrt[5]{2} = 2 \sqrt[5]{2}](/latexrender/pictures/c84681e692e197ae68842a834b5ee1a1.png)
, mas ao contrário. Eu estava tentando te ajudar não respondendo a perguntar pra você, mas fazendo você pensar a respeito e chegar na resposta você mesmo para que você desenvolvesse habilidade e raciocínio que lhe servissem úteis mais pra frente. Porém, o você me vem com sérias grosserias e diz:
gigante2010 escreveu:Eu quero que RESOLVAM!
Você não é NINGUÉM! Você é um NADA! Quem é você para querer que nós resolvamos as suas listas de exercício? Você não veio pedir ajuda, você veio aqui para que resolvêssemos seus problemas pra você. Isso aqui é uma ajuda VOLUNTÁRIA, e caso você não saiba o significado dessa palavra, quer dizer aqui que ninguém é PAGO pra ficar aqui o dia inteiro aguentando CRIANÇAS COMO VOCÊ, do ENSINO FUNDAMENTAL, dizendo que QUEREM que nós resolvamos seus problemas. Daqui pra frente, quero deixar bem claro que eu me recuso a te ajudar. Eu também sou ninguém, eu tenho uma vida, eu faço uma faculdade, e mesmo assim eu me disponho a vir aqui e gastar meu tempo para ajudar outras pessoas que tem dificuldade, e sabe o que eu sou obrigado a ver? Não, melhor, todos os colaboradores do fórum tem suas vidas e seus afazeres, e mesmo assim vem aqui de bom humor para ajudar gente como você, que responde assim:gigante2010 escreveu:Eu quero que RESOLVAM!
Você não é um gigante, muito pelo contrário, você é alguém minúsculo, pois lhe falta muita HUMILDADE e SIMPLICIDADE, vindo aqui com tal ARROGÂNCIA, DEMANDANDO coisas.
Você, novamente, é um NADA.Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por gigante2010 » Sex Out 22, 2010 23:15
por gigante2010 » Sex Out 22, 2010 23:15
Não só tem vc oferecendo ajuda no mundo. Reflita.
-
gigante2010
-
 por DanielRJ » Ter Out 26, 2010 16:17
por DanielRJ » Ter Out 26, 2010 16:17
gigante2010 escreveu:Não só tem vc oferecendo ajuda no mundo. Reflita.
Deixa de ser abusado, ninguem tem obrigação de fazer seus trabalhos de casa, se perguntaram a você "Se sabia fatorar"
é para forçar sua mente a pensar e não subestima=lo.O Objetivo do forum mais uma vez frisando aqui é ajudar você a progredir sem essa de trabalinho de casa.
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por victoreis1 » Ter Out 26, 2010 16:30
por victoreis1 » Ter Out 26, 2010 16:30
é muito palhaço mesmo.. e ainda se auto-intitula gigante.. pft
-
victoreis1
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Qua Out 20, 2010 14:49
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Luanita » Dom Mai 15, 2011 13:13
por Luanita » Dom Mai 15, 2011 13:13
Ola,
Bom pessoal, antes de tudo, li todas as trocas de informaçoes deste topico e vi que chegou a um estado lamentavel,
pois entendi que algumas pessoas sao despreparadas até para fazer perguntas, mas espero que os voluntarios ainda
continuem com o bonito trabalho de esclarecer duvidas, principalmente na area de exatas, pois a cada dia fica mais
escasso . Estudo Engenharia, tenho serias dificulades, pois a minha base de matematica na infancia foi muito pobre,
e naquele tempo, o acesso a internet era impossivel, nao existiam voluntarios para esclarecer duvidas, nossos pais,
que na maioria da vezes tinham até menos conhecimentos que nòs, nao podiam nos ensinar, sentar conosco e explicar
as materias, entao, eu antes de tudo gostaria de agradecer aos VOLUNTARIOS, por estarem aqui nos ajudando, conheci
este site hoje 15/05/11, mas pode ter certeza que vou passar aos colegas da faculdade que como eu sofrem com duvidas
e nao encontramos profissionais que nos possam orientar, devido a escassez de gente capacitada nesta area. A matematica
nao é uma brincadeira, ela é até bonita quando voce entende o X da questao. Gostaria de ter tempo suficiente pra me
dedicar inteiramente à ela. De qualquer forma, espero que o trabalho de voces seja reconhecido, o Voluntariado por si sò,
é um GRANDE gesto

!
-
Luanita
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Mai 15, 2011 12:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Petroleo
- Andamento: cursando
 por Luanita » Dom Mai 15, 2011 13:23
por Luanita » Dom Mai 15, 2011 13:23
Tenho uma duvida cruel com um exercicio que encontrei em uma das provas de concurso, como tneho interesse em prestar concurso, inclusive ENEM deste ano,
procurei colegas e até professores que me ajudassem, mas nao tive exito, repasso à vocs, se puderem esclarecer como começar o exercicio ja é um grande passo...
2^2003-9^1001/4^1001-3^2003 + 2^2002-9^1001/4^1001-3^2003
nunca antes vi expoentes tao altos... nao sei nem como começar !!!
obrigada.
-
Luanita
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Mai 15, 2011 12:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Petroleo
- Andamento: cursando
Voltar para Tópicos sem Interação (leia as regras)
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Potencia e raizes
por ginrj » Ter Mar 10, 2009 20:24
- 4 Respostas
- 8199 Exibições
- Última mensagem por ginrj

Qua Mar 11, 2009 19:32
Álgebra Elementar
-
- [Série de potÊncia] Expansão de séries de potência
 por Adonias 7 » Qua Jun 01, 2016 09:05
por Adonias 7 » Qua Jun 01, 2016 09:05
- 0 Respostas
- 3686 Exibições
- Última mensagem por Adonias 7

Qua Jun 01, 2016 09:05
Sequências
-
- Potência de potência... não sei ao certo se entendi...
por Vennom » Sáb Fev 20, 2010 10:42
- 3 Respostas
- 3769 Exibições
- Última mensagem por mottasky

Ter Out 04, 2011 02:03
Álgebra Elementar
-
- [Potencia] soma de potencia com letras
por carla villela » Qui Mar 01, 2012 21:04
- 8 Respostas
- 8604 Exibições
- Última mensagem por carla villela

Qui Mar 01, 2012 22:18
Sistemas de Equações
-
- [raízes de números complexos] Raízes de uma equação com grau
por karenfreitas » Seg Ago 22, 2016 19:08
- 1 Respostas
- 8111 Exibições
- Última mensagem por adauto martins

Sáb Ago 27, 2016 16:11
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\frac{3}{\sqrt[2]{3}-2} \frac{3}{\sqrt[2]{3}-2}](/latexrender/pictures/c9d6af1dc7c19f439531dc37188c2213.png)
![\sqrt[5]{64} \sqrt[5]{64}](/latexrender/pictures/4d396534f3dff06bb97e27de112259b5.png)
![\frac{10 \sqrt[2]{9}}{5\sqrt[2]{3}} \frac{10 \sqrt[2]{9}}{5\sqrt[2]{3}}](/latexrender/pictures/2d555d11a8844f00aebe2fe94acf40a8.png)
![\frac{\sqrt[2]{27}}{4\sqrt[3]{2}} \frac{\sqrt[2]{27}}{4\sqrt[3]{2}}](/latexrender/pictures/3daa69230b9b12671bd1439125ff805a.png)
![\sqrt[3]{-54} \sqrt[3]{-54}](/latexrender/pictures/80c97ad00ad0f51e1f323ee333b4e2a8.png) << como é a fatoração dela?
<< como é a fatoração dela?  quando
quando  << não consigo resolver.
<< não consigo resolver.
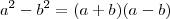 . O segundo, fatore 64. O terceiro, elimine a raíz do denominador. No quarto, fatore 27 e depois faça
. O segundo, fatore 64. O terceiro, elimine a raíz do denominador. No quarto, fatore 27 e depois faça ![\sqrt[3]{2} \sqrt[3]{2}](/latexrender/pictures/9a132a1fa0d4f51451f00801ccbfe963.png) virar
virar  . Para o outro, lembre-se que
. Para o outro, lembre-se que ![\sqrt[3]{-a} = - \sqrt[3]{a} \sqrt[3]{-a} = - \sqrt[3]{a}](/latexrender/pictures/50d9645b37590b4d92e72b65dc742fa1.png) e fatore. No último, lembre-se propriedades de expoentes, sinais e coloque
e fatore. No último, lembre-se propriedades de expoentes, sinais e coloque 

 e que ficaria
e que ficaria ![\sqrt[5]{64} = \sqrt[5]{2^6} = \sqrt[5]{2^5} \sqrt[5]{2} = 2 \sqrt[5]{2} \sqrt[5]{64} = \sqrt[5]{2^6} = \sqrt[5]{2^5} \sqrt[5]{2} = 2 \sqrt[5]{2}](/latexrender/pictures/c84681e692e197ae68842a834b5ee1a1.png) , mas ao contrário. Eu estava tentando te ajudar não respondendo a perguntar pra você, mas fazendo você pensar a respeito e chegar na resposta você mesmo para que você desenvolvesse habilidade e raciocínio que lhe servissem úteis mais pra frente. Porém, o você me vem com sérias grosserias e diz:
, mas ao contrário. Eu estava tentando te ajudar não respondendo a perguntar pra você, mas fazendo você pensar a respeito e chegar na resposta você mesmo para que você desenvolvesse habilidade e raciocínio que lhe servissem úteis mais pra frente. Porém, o você me vem com sérias grosserias e diz:

 !
!
 } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: