 por Thassya » Seg Out 11, 2010 21:46
por Thassya » Seg Out 11, 2010 21:46
Por favor me ajudem com essa questão!!!
URGENTEEEEEEEEEEEEEEE
Uma fatia de 3cm de espessura é cortada de um cubo, deixando um volume de 108cm CUBICOS . Encontre o
comprimento do lado do cubo original
-
Thassya
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Qui Mai 21, 2009 23:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matematica
- Andamento: cursando
 por MarceloFantini » Ter Out 12, 2010 04:21
por MarceloFantini » Ter Out 12, 2010 04:21
Vamos chamar o lado do novo cubo de

. Então

, e o lado do volume antigo será

.
![a = \sqrt[3]{108} = 3 \sqrt[3]{2^2} a = \sqrt[3]{108} = 3 \sqrt[3]{2^2}](/latexrender/pictures/0e90d263735a2e241d251d452e96f600.png)
e o lado
![a+3 = 3 \sqrt[3]{2^2} + 3 = 3(1 + \sqrt[3]{2^2}) a+3 = 3 \sqrt[3]{2^2} + 3 = 3(1 + \sqrt[3]{2^2})](/latexrender/pictures/1d4273237c2a76b0053243f742335595.png)
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Augusto Evaristo » Sáb Out 16, 2010 01:33
por Augusto Evaristo » Sáb Out 16, 2010 01:33
Fantini escreveu:Vamos chamar o lado do novo cubo de

. Então

, e o lado do volume antigo será

.
![a = \sqrt[3]{108} = 3 \sqrt[3]{2^2} a = \sqrt[3]{108} = 3 \sqrt[3]{2^2}](/latexrender/pictures/0e90d263735a2e241d251d452e96f600.png)
e o lado
![a+3 = 3 \sqrt[3]{2^2} + 3 = 3(1 + \sqrt[3]{2^2}) a+3 = 3 \sqrt[3]{2^2} + 3 = 3(1 + \sqrt[3]{2^2})](/latexrender/pictures/1d4273237c2a76b0053243f742335595.png)
Cara Thassya e Caro Fantini,
É um prazer trazer a minha participação para essa questão.
Tenho a corrigir humildemente um tetalhe, e peço desde já sua permissão.
Quando a questão chama a figura geométrica de cubo, implica em dizer que ela tem as arestas iguais e seu volume será dado pela seguinte fórmula:

No entanto, a questão diz que desse cubo é retirada uma fatia, observemos bem, uma fatia e tão somente uma fatia, que significa seccionar o cubo, e no tamanho de 3 cm de espessura, o que implica dizer que interfere em apenas uma das medidas da figura que passará a se chamar paralelepípedo. Corrijam-me se eu estiver errado. Logo a medida do seu volume será dada pelo produto da base com a altura e a profundidade será dada agora pela seguinte fórmula:

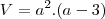

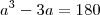

Agora deixo para você desenvolver essa equação cúbica por Cardano.
Foi um prazer ajudar.
Matemática não é uma arte
É a linguagem universal
Arte é conhece-la!
-

Augusto Evaristo
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Sex Out 15, 2010 18:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Elcioschin » Sáb Out 16, 2010 18:50
por Elcioschin » Sáb Out 16, 2010 18:50
O Augusto está com razão, com duas ressalvas:
O correto é 108 e não é 180.
Não é necessário Cardano:
a³ - 3a² - 108 = 0 ----> 108 = 2²*3³ ----> Divisores de 108: + - 1, 2, 3, 4, 6,12, 27, 36, 54, 108,
(a - 3)*a² = 108 ----> (a - 3)*a² = 3*36 ----> (a - 3)*a² = 3*6² ----> a = 6
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Augusto Evaristo » Dom Out 17, 2010 16:06
por Augusto Evaristo » Dom Out 17, 2010 16:06
Elcioschin escreveu:O Augusto está com razão, com duas ressalvas:
O correto é 108 e não é 180.
Não é necessário Cardano:
a³ - 3a² - 108 = 0 ----> 108 = 2²*3³ ----> Divisores de 108: + - 1, 2, 3, 4, 6,12, 27, 36, 54, 108,
(a - 3)*a² = 108 ----> (a - 3)*a² = 3*36 ----> (a - 3)*a² = 3*6² ----> a = 6
Olá Elciochin,
Agradeço pelas suas ressalvas. É esse o espírito desse forum.
Parabéns!
Matemática não é uma arte
É a linguagem universal
Arte é conhece-la!
-

Augusto Evaristo
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Sex Out 15, 2010 18:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Dom Out 17, 2010 16:14
por MarceloFantini » Dom Out 17, 2010 16:14
E eu o agradeço por ter consertado a resolução. Obrigado.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Caroline Maul » Qua Out 20, 2010 21:20
por Caroline Maul » Qua Out 20, 2010 21:20
Elcioschin escreveu:O Augusto está com razão, com duas ressalvas:
O correto é 108 e não é 180.
Não é necessário Cardano:
a³ - 3a² - 108 = 0 ----> 108 = 2²*3³ ----> Divisores de 108: + - 1, 2, 3, 4, 6,12, 27, 36, 54, 108,
(a - 3)*a² = 108 ----> (a - 3)*a² = 3*36 ----> (a - 3)*a² = 3*6² ----> a = 6
Perdoe minha ignorância, mas no final o que vc fez... pegou os termos elevados ao mesmo expoente e igualou???
Assim: a-3=3 -> a=6 ou a²=6²->a=6?? Caso foi isso, esse método pode sempre ser usado em multiplicações no estilo dessa??
O negócio dos divisores foi só pra encontrar valores que pudessem ser usados dessa forma??
Desde já agradeço a resposta!!
-
Caroline Maul
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Out 20, 2010 21:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Física / Engenharia
- Andamento: cursando
 por MarceloFantini » Qua Out 20, 2010 21:26
por MarceloFantini » Qua Out 20, 2010 21:26
Não, não pode fazer isso sempre. Ele fez isso porque assumiu que a solução era inteira.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Caroline Maul » Qua Out 20, 2010 21:45
por Caroline Maul » Qua Out 20, 2010 21:45
Fantini escreveu:Não, não pode fazer isso sempre. Ele fez isso porque assumiu que a solução era inteira.
Mas foi isso mesmo que ele fez, né? E sempre que eu puder assumir como sendo inteira posso usar isso???
Editado pela última vez por
Caroline Maul em Qua Out 20, 2010 21:58, em um total de 1 vez.
-
Caroline Maul
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Out 20, 2010 21:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Física / Engenharia
- Andamento: cursando
 por MarceloFantini » Qua Out 20, 2010 21:48
por MarceloFantini » Qua Out 20, 2010 21:48
Caroline, não se bitole nisso. Não é regra geral.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- cubo
 por camilalindynha » Ter Dez 11, 2007 18:56
por camilalindynha » Ter Dez 11, 2007 18:56
- 1 Respostas
- 6810 Exibições
- Última mensagem por admin

Ter Dez 11, 2007 20:05
Geometria Espacial
-
- Cubo (FEI - SP)
 por Ananda » Qua Fev 27, 2008 16:05
por Ananda » Qua Fev 27, 2008 16:05
- 3 Respostas
- 5107 Exibições
- Última mensagem por agp16

Dom Nov 08, 2009 21:42
Geometria Espacial
-
- Cubo
por Neperiano » Qui Fev 12, 2009 11:15
- 6 Respostas
- 3586 Exibições
- Última mensagem por Neperiano

Sex Fev 13, 2009 13:57
Geometria Espacial
-
- Cubo
 por Pri Ferreira » Qua Mar 21, 2012 14:17
por Pri Ferreira » Qua Mar 21, 2012 14:17
- 1 Respostas
- 1632 Exibições
- Última mensagem por LuizAquino

Ter Mar 27, 2012 18:05
Geometria Espacial
-
- cubo
por von grap » Qua Mai 09, 2012 18:36
- 0 Respostas
- 1921 Exibições
- Última mensagem por von grap

Qua Mai 09, 2012 18:36
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 . Então
. Então  , e o lado do volume antigo será
, e o lado do volume antigo será  .
. ![a = \sqrt[3]{108} = 3 \sqrt[3]{2^2} a = \sqrt[3]{108} = 3 \sqrt[3]{2^2}](/latexrender/pictures/0e90d263735a2e241d251d452e96f600.png) e o lado
e o lado ![a+3 = 3 \sqrt[3]{2^2} + 3 = 3(1 + \sqrt[3]{2^2}) a+3 = 3 \sqrt[3]{2^2} + 3 = 3(1 + \sqrt[3]{2^2})](/latexrender/pictures/1d4273237c2a76b0053243f742335595.png)


. Então
, e o lado do volume antigo será
.
e o lado


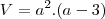

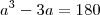










![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.