Queria ajuda do pessoal para resolver esta questão
Augusto emprestou R$ 30.000,00 a César, à taxa de juros de 10% ao mês. Eles combinaram que o saldo devedor seria
calculado a juros compostos no número inteiro de meses e, a seguir, corrigido a juros simples, com a mesma taxa de
juros, na parte fracionária do período, sempre considerando o mês com 30 dias. Para quitar a dívida 2 meses e 5 dias após o empréstimo, César deve pagar a Augusto, em reais,
(A) 39.930,00
(B) 39.600,00
(C) 37.026,00
(D) 36.905,00
(E) 36.300,00
Como estabelecer os valores ? Não sei por onde começar...
Obrigada !!!
após 2 meses, partindo do capital 
, com a taxa de juros compostos 
de 10%: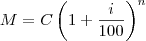
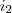proporcional aos 5 dias. Faça uma regra de três:
, no final, multiplique o montante por 
.
: o número de períodos considerados (meses, anos etc)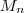
: o montante após 
, temos: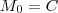
, aplicamos pela primeira vez a taxa de juros:
:
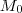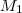em evidência:
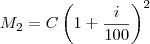
em evidência: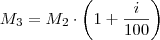
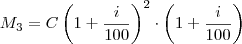
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.