 por andrelpti » Dom Out 10, 2010 18:04
por andrelpti » Dom Out 10, 2010 18:04
Pessoal boa tarde !!
Será que alguém poderiam me ajudar com estas duas equações.
1ª)
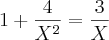
2ª)
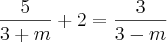
Desde de já agradeço a ajuda.
-
andrelpti
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Dom Set 05, 2010 14:21
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Redes
- Andamento: cursando
 por MarceloFantini » Dom Out 10, 2010 23:35
por MarceloFantini » Dom Out 10, 2010 23:35
Na primeira as únicas respostas são 1 e 4, pois

já que está no denominador.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por DanielRJ » Seg Out 11, 2010 00:54
por DanielRJ » Seg Out 11, 2010 00:54
Opa brigado.
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ajuda na equação do 1 grau
por zekinha » Seg Jun 27, 2011 00:38
- 12 Respostas
- 7836 Exibições
- Última mensagem por Fabio Cabral

Ter Jun 28, 2011 00:43
Álgebra Elementar
-
- Ajuda equação de 2º grau
por qwepoi678 » Ter Ago 28, 2012 16:46
- 2 Respostas
- 2187 Exibições
- Última mensagem por MarceloFantini

Qua Ago 29, 2012 09:59
Equações
-
- Ajuda equação de 2º grau
por MarceloFantini » Ter Ago 28, 2012 19:22
- 0 Respostas
- 967 Exibições
- Última mensagem por MarceloFantini

Ter Ago 28, 2012 19:22
Equações
-
- ajuda com equaçao de segundo grau
por jmontenegro » Dom Fev 19, 2012 12:04
- 1 Respostas
- 1576 Exibições
- Última mensagem por fraol

Dom Fev 19, 2012 22:58
Funções
-
- Equação do segundo grau, ajuda.
por LuizCarlos » Dom Mai 13, 2012 13:02
- 2 Respostas
- 1979 Exibições
- Última mensagem por LuizCarlos

Dom Mai 13, 2012 17:17
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
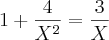
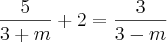

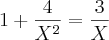
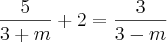

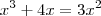
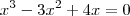

 ou
ou  ou
ou 

![5(3-m)+2[(3+m)(3-m)]=3(3+m) 5(3-m)+2[(3+m)(3-m)]=3(3+m)](/latexrender/pictures/49ec12d9a84ae6ab822125410797ef98.png)
![15-5m+2[3^2-m^2]=9+3m 15-5m+2[3^2-m^2]=9+3m](/latexrender/pictures/e720a9f1feb8a6c240b8a66a0d41166e.png)

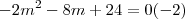
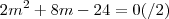

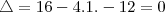



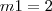 e
e 

 já que está no denominador.
já que está no denominador.



 .
.



