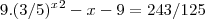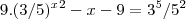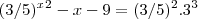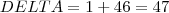por natanskt » Sex Out 08, 2010 11:39
por natanskt » Sex Out 08, 2010 11:39
5-)a soma e o produto das raizes da equação

a-)1 e -12
b-)7 e 12
c-)-2 e -8
d-)-1 e 12
e-)7 e 10
obs:o expoente
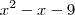
esta em cima do 3 é pq não ficou em cima direito,tentei resolver mais nem sei como começar,por favor ,deixe nos minimos detalhes,pra mim conseguir intender!
valeu pessoal!
-
natanskt
- Colaborador Voluntário

-
- Mensagens: 176
- Registrado em: Qua Out 06, 2010 14:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nenhum
- Andamento: cursando
 por DanielRJ » Sex Out 08, 2010 16:36
por DanielRJ » Sex Out 08, 2010 16:36
Vamos por parte.pegamos os numeradores.


multiplique e cortamos as bases.
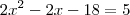
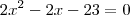
Bom cheguei a isso mas não consigo encontrar as raizes.
Vamos ver se alguem nos ajuda;D
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Loretto » Sex Out 08, 2010 17:49
por Loretto » Sex Out 08, 2010 17:49
-
Loretto
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Dom Jul 25, 2010 01:35
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: exatas
- Andamento: cursando
 por Elcioschin » Sex Out 08, 2010 17:57
por Elcioschin » Sex Out 08, 2010 17:57
O Loretto resolveu certo, porém o Latex ficou deformado
9*(3/5)^(x² - x - 9) = 243/125 ----> Divide por 9
(3/5)^(x² - x - 9) = 27/125
(3/5)^(x² - x - 9) = (3/5)^3
x² - x - 9 = 3
x² - x - 12 = 0
Soma das raízes = 1
Produto das raízes = -12
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Loretto » Sex Out 08, 2010 17:59
por Loretto » Sex Out 08, 2010 17:59
Obrigado Elcioschin !! Ainda num sei usar muito bem o latex !! Principalmente quando colocar DELTA e algumas outras notações, mas vou me acostumando. Abraço!
-
Loretto
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Dom Jul 25, 2010 01:35
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: exatas
- Andamento: cursando
 por natanskt » Sex Out 08, 2010 18:18
por natanskt » Sex Out 08, 2010 18:18
pq vc dividiu por 9?
eu posso fazer isso nas outras questão?
da onde saiu esse 9
eu sou burro de matematica
-
natanskt
- Colaborador Voluntário

-
- Mensagens: 176
- Registrado em: Qua Out 06, 2010 14:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nenhum
- Andamento: cursando
 por natanskt » Sex Out 08, 2010 18:21
por natanskt » Sex Out 08, 2010 18:21
não intendi pq só o numerador foi divido por 9
-
natanskt
- Colaborador Voluntário

-
- Mensagens: 176
- Registrado em: Qua Out 06, 2010 14:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nenhum
- Andamento: cursando
 por natanskt » Sex Out 08, 2010 18:23
por natanskt » Sex Out 08, 2010 18:23
obrigado a vcs todos,eu intendi...(eu acho)
muito obrigado
DEUS ABENÇOE VCS
-
natanskt
- Colaborador Voluntário

-
- Mensagens: 176
- Registrado em: Qua Out 06, 2010 14:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nenhum
- Andamento: cursando
 por Elcioschin » Sex Out 08, 2010 21:05
por Elcioschin » Sex Out 08, 2010 21:05
natanskt
O final da sua frase me preocupa: "Eu acho"
Vamos fazer vc ter certeza
Para facilitar o entendimento com a escrita, vou fazer A = (3/5)^(x² - x - 9):
9*A = 243/125
9*A = 9*27/125 ----> Dividindo ambos os membros por 9:
A = 27/125 ----> A = 3³/5³ ----> A = (3/5)³ ---> Entendeu agora porque no 2º membro foi dividido por 9 apenas o numerador ?
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por DanielRJ » Sex Out 08, 2010 22:37
por DanielRJ » Sex Out 08, 2010 22:37
Eu não poderia trabalhar apenas com os numeradores?
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Elcioschin » Sex Out 08, 2010 22:55
por Elcioschin » Sex Out 08, 2010 22:55
Daniel
Como regra geral não.
Particularmente neste caso é possível pelo seguinte:
9*[3/5]^(x² - x - 9) = 243/125
9*[3/5]^(x² - x - 9) = 9*27/125 ----> Dividindo mbos os mebros por 9
[3/5]^(x² - x - 9) = 27/125
[3/5]^(x² - x - 9) = (3/5)^3
Note agora que as bases das potências são iguais. Neste caso tanto faz qual é a base (poderia ser 3, 5, 5/3, 1000, etc).
Por isto eu pode-se igualar os expoentes como se considerássemos APENAS o numerador 5
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (ESPCEX) Equacao exponencial
por natanskt » Qui Out 07, 2010 20:26
- 2 Respostas
- 2729 Exibições
- Última mensagem por natanskt

Sex Out 08, 2010 09:37
Funções
-
- (ESPCEX) Equacao exponencial
por natanskt » Qui Out 07, 2010 20:35
- 3 Respostas
- 2768 Exibições
- Última mensagem por diogosoullost

Sáb Ago 03, 2013 23:15
Funções
-
- (ESPCEX) Equação logaritmica
por natanskt » Seg Out 11, 2010 16:16
- 3 Respostas
- 2178 Exibições
- Última mensagem por MarceloFantini

Qua Out 13, 2010 13:50
Logaritmos
-
- (ESPCEX) Equação logaritmica
por natanskt » Seg Out 11, 2010 16:23
- 3 Respostas
- 1752 Exibições
- Última mensagem por DanielRJ

Seg Out 11, 2010 18:39
Logaritmos
-
- (ESPCEX) Equação logaritmica
por natanskt » Seg Out 11, 2010 16:50
- 2 Respostas
- 5653 Exibições
- Última mensagem por DanielRJ

Seg Out 11, 2010 18:25
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

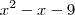 esta em cima do 3 é pq não ficou em cima direito,tentei resolver mais nem sei como começar,por favor ,deixe nos minimos detalhes,pra mim conseguir intender!
esta em cima do 3 é pq não ficou em cima direito,tentei resolver mais nem sei como começar,por favor ,deixe nos minimos detalhes,pra mim conseguir intender!

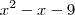 esta em cima do 3 é pq não ficou em cima direito,tentei resolver mais nem sei como começar,por favor ,deixe nos minimos detalhes,pra mim conseguir intender!
esta em cima do 3 é pq não ficou em cima direito,tentei resolver mais nem sei como começar,por favor ,deixe nos minimos detalhes,pra mim conseguir intender!

 multiplique e cortamos as bases.
multiplique e cortamos as bases.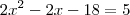
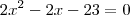 Bom cheguei a isso mas não consigo encontrar as raizes.
Bom cheguei a isso mas não consigo encontrar as raizes.