P.A de razão sendo outra P.A, ajuda

[MariMari]

Bom pessoal, essa é a minha primeira experiência com o fórum, boa tarde
Avancei um pouco nessa questão, porem não tive muito sucesso em alguns pontos.

Números naturais ímpares estão dispostos dessa forma

1
3 5
7 9 11
13 15 17 19
21 23 25 27 29

O número que inicia a 51ª linha é ?
(A) 2549 (B) 2551 (C) 2553 (D) 2555 (E) 2547

Bom, cheguei a conclusão de que essa primeira linha esta em progressão aritmética de razão igual a outra progressão aritmética.




Num momento de quase inércia mental, eu tive um presságio sobre essa razão. Pensei '' na segunda P.A o correto será ao invés de ''
Isso está correto?

Mas voltando... Observando e aplicando essa resolução a valores já conhecidos por mim, já mostrados nessa disposição dos números, percebi que se trocasse por apenas o da equação '' base '', daria o valor que eu queria achar, ficando assim:





Usando isso, eu encontrei o valor de (B) 2551

Essa resposta esta correta?
Eu provei pra apenas os valores testados que , como provar isso matematicamente para todos os valores da P.A?

[Douglasm]

Olá Mari. Deste jeito inicial, dará errado, pois você estará considerando a razão naquele determinado termo, e contará como se todos os outros termos tivessem sido somados utilizando aquela mesma razão. Você deve é somar todos os termos que tem, até chegar no 51º. Isso é simples, veja só:

3 = 1 + 2

7 = 1 + 2 + 4

13 = 1 + 2 + 4 + 6

21 = 1 + 2 + 4 + 6 + 8

É evidente que o enésimo termo será igual a 1 mais a soma de uma progressão de (n-1) termos e razão 2. Logo:

[MariMari]

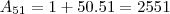
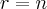Obrigada Douglas. Hoje cedo, eu refletindo um pouco sobre essa questão, percebi que estava errada. Comecei a fazer novamente e cheguei a , o que se encaixa bem na sua resolução.