 por Tiago » Sex Set 03, 2010 15:59
por Tiago » Sex Set 03, 2010 15:59
Em épocas de prêmio acumulado, fica-se a pergunta, como seria a combinação de uma sequencia de numeros para fechamento de um acerto.
Bom, com essa curiosidade fui atrás, e não obtive muitos resultados.
Vi um fechamento de 18 numeros com o acerto dos 6 numeros, no minimo o acerto de uma quadra, com 42 jogos.
E outro e 12 numeros, e acerto de 6 numeros com no minimo acerto de uma quadra.
è o chamado fechamento reduzido.
Existem varios softwares que fazem, mais o eu gostaria de saber e fazer o calculo, e peço ajuda, pelo menos para começar...
Este é o exemplo de 12 numeros.
1 2 3 4 5 6
1 2 3 7 8 9
1 2 3 10 11 12
4 5 6 7 8 9
4 5 6 10 11 12
7 8 9 10 11 12
Observem que se quais quer de 6 numeros escolhidos entre 1 e 12, no minimo uma quadra.
Valeu!!
-
Tiago
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Sáb Set 12, 2009 18:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: cursando
 por alexandre32100 » Sex Set 03, 2010 16:05
por alexandre32100 » Sex Set 03, 2010 16:05
Tiago, a que cálculo, mais precisamente você quer chegar? Das possibilidades de acerto de pelo menos um quadra ou o quê?
-
alexandre32100
-
 por Tiago » Sex Set 03, 2010 19:42
por Tiago » Sex Set 03, 2010 19:42
Olá alexandre32100.
Eu gostaria de aprender a fazer um fechamento com no minimo uma quadra.
Eu vi com 12 e 18 dezenas.
Se por acaso eu quizesse fazer um fechamento com 20 dezenas com jogo tipo megasena de 6 numeros, com no minimo de acerto de 4 numeros "quadra" se caso as 6 dezenas sorteadas estivessem entre as 20 escolhidas.
Não que ver o fechamento, quero aprender a fazer o calculo do fechamento e ver quantas cartelas seriam necessarias, para cada tipo de fechamento que eu escolhesse,como nesse exemplo citado 20 dezenas.
Abraços.
-
Tiago
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Sáb Set 12, 2009 18:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: cursando
 por Tiago » Seg Set 06, 2010 23:32
por Tiago » Seg Set 06, 2010 23:32
Bom , agora que passou a megasena acumulada, alguem me ajude a começar esse calculo.
Se vc não sabe o calculo completo,poste o que vc sabe, blz, eu preciso começar a entender e já pode ser um começo.
Valeu!!!
-
Tiago
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Sáb Set 12, 2009 18:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: cursando
 por amiltonbicas » Sex Set 17, 2010 11:28
por amiltonbicas » Sex Set 17, 2010 11:28
Aproveitamento o tópico, gostaria de sanar uma dúvida que surgiu quando eu discutia com alguns colegas meus.
Um jogo da mega sena onde eu posso marcar 6 números custa R$2.00 e um jogo onde eu posso marcar 10 números custa R$420.00. Logo veio a dúvida, qual a maior chance de eu ganhar, probabilisticamente falando? Fazendo um jogo de 10 números ou 210 jogos de 6 números. Gostaria de saber os cálculos para isso, para que eu possa mostrar a todos.
Desde já obrigado
-
amiltonbicas
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Set 17, 2010 11:17
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Informática
- Andamento: cursando
 por alexandre32100 » Sex Set 17, 2010 21:04
por alexandre32100 » Sex Set 17, 2010 21:04
Num jogo normal, a sua chance é de
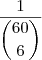
, assim, fazendo
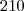
jogos distintos, as chances aumentam para
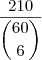
.
Agora, fazendo um jogo de dez números, podemos contar qualquer combinação de
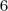
números dentre os

escolhidos como
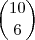
, assim suas chances são de
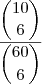
.
O engraçado é que
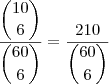
, independendo do método que você escolher, suas chances são as mesmas. Acho que por isso do valor já ser de

reais.

Espero ter sido útil.
-
alexandre32100
-
 por felipecchaves » Dom Set 19, 2010 03:27
por felipecchaves » Dom Set 19, 2010 03:27
Acho que esse não é o lugar certo pra essa pergunta, mas vou aproveitar o tópico.
Por exemplo:
Se eu pegar 9 números e fizer todas as combinações possíveis da um total de 84 jogos e o valor da aposta é de R$ 168,00. O que é o mesmo que eu jogar 9 números na mesma cartela.
No caso de eu jogar 9 números na mesma cartela, se eu ganhar uma quadra, por exemplo, eu recebo proporcional ou recebo apenas como um jogo?
Caso o valor do premio seja proporcional é melhor jogar os 9 na mesma cartela, porque nas 84 combinações possíveis nem todas terão uma quadra. Eu to certo nisso?
-
felipecchaves
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Set 19, 2010 03:07
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Rogerio Murcila » Dom Set 19, 2010 22:30
por Rogerio Murcila » Dom Set 19, 2010 22:30
alexandre32100 escreveu:Num jogo normal, a sua chance é de
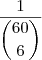
, assim, fazendo
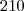
jogos distintos, as chances aumentam para
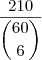
.
Agora, fazendo um jogo de dez números, podemos contar qualquer combinação de
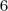
números dentre os

escolhidos como
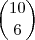
, assim suas chances são de
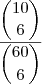
.
O engraçado é que
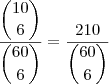
, independendo do método que você escolher, suas chances são as mesmas. Acho que por isso do valor já ser de

reais.

Espero ter sido útil.
Olá Alexandre,
Em minhas contas deu um pouco diferente:
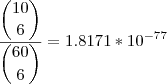
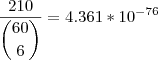
Será que fiz alguma conta errada? Confere ai.

-
Rogerio Murcila
- Usuário Parceiro

-
- Mensagens: 64
- Registrado em: Sex Set 10, 2010 16:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eletronica / Quimica / Adm
- Andamento: formado
 por alexandre32100 » Seg Set 20, 2010 12:42
por alexandre32100 » Seg Set 20, 2010 12:42
Rogério,
pode depender do método que você utilizou para calcular a divisão ou o binômio, mas acompanhe meus cálculos:
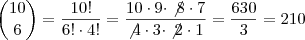
Por afirmei que
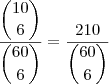
.
Se quiser usar uma representação decimal:
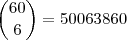
E também
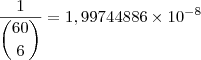
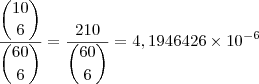
-
alexandre32100
-
 por Rogerio Murcila » Seg Set 20, 2010 14:10
por Rogerio Murcila » Seg Set 20, 2010 14:10
alexandre32100 escreveu:Rogério,
pode depender do método que você utilizou para calcular a divisão ou o binômio, mas acompanhe meus cálculos:
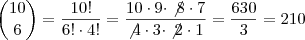
Por afirmei que
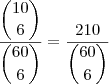
.
Se quiser usar uma representação decimal:
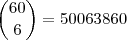
E também
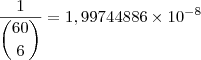
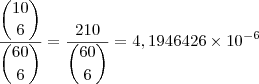
Olá Alexandre,
Realmente ai está a diferença veja abaixo:
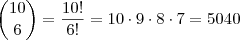
ou
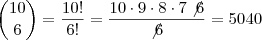
ou
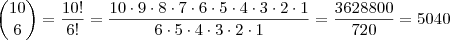
-
Rogerio Murcila
- Usuário Parceiro

-
- Mensagens: 64
- Registrado em: Sex Set 10, 2010 16:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eletronica / Quimica / Adm
- Andamento: formado
 por alexandre32100 » Seg Set 20, 2010 19:20
por alexandre32100 » Seg Set 20, 2010 19:20
Pois é, Rogério, vale lembrar que a fórmula algébrica para o
Binômio de Newton é
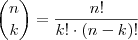
, por isso da diferença entre as soluções.
Abraços,
-
alexandre32100
-
 por alexandre32100 » Seg Set 20, 2010 19:39
por alexandre32100 » Seg Set 20, 2010 19:39
felipecchaves escreveu:Acho que esse não é o lugar certo pra essa pergunta, mas vou aproveitar o tópico.
Por exemplo:
Se eu pegar 9 números e fizer todas as combinações possíveis da um total de 84 jogos e o valor da aposta é de R$ 168,00. O que é o mesmo que eu jogar 9 números na mesma cartela.
No caso de eu jogar 9 números na mesma cartela, se eu ganhar uma quadra, por exemplo, eu recebo proporcional ou recebo apenas como um jogo?
Caso o valor do premio seja proporcional é melhor jogar os 9 na mesma cartela, porque nas 84 combinações possíveis nem todas terão uma quadra. Eu to certo nisso?
Realmente isso é curioso. Mas acho que o prêmio não é proporcional à aposta.
Se você faz uma aposta de nove números e sejam sorteados seis dos quais quatro são iguais aos apostados (a quadra), você recebe o prêmio da quadra. Se não, realmente, seria mais vantagem jogarmos os nove números de vez, mas se for como estou supondo, é mais vantajoso (e bem mais trabalhoso) fazer as

apostas separadamente.

Quanto à questão dos valores das apostas, queria mostrar algo curioso:
Suponha que você queira apostar
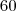
números numa só cartela. Pelo que já foi visto nesse tópico, o preço seria de
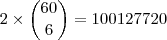
reais. Fica a dica: da próxima vez que a Mega Sena acumulada ultrapassar este valor, aposte e torça para ganhar o prêmio sozinho.

-
alexandre32100
-
 por Rogerio Murcila » Seg Set 20, 2010 22:22
por Rogerio Murcila » Seg Set 20, 2010 22:22
Perfeito Alexandre,

Só esqueci da regra que mancada hehehehe
É ficar parado no tempo dá nisso e matemática não tem perdão.



Grato e abraço amigo.

-
Rogerio Murcila
- Usuário Parceiro

-
- Mensagens: 64
- Registrado em: Sex Set 10, 2010 16:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eletronica / Quimica / Adm
- Andamento: formado
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problema probabilidade MEGASENA!
por camilesfnogueira » Ter Nov 23, 2010 00:00
- 2 Respostas
- 1942 Exibições
- Última mensagem por camilesfnogueira

Ter Nov 23, 2010 17:11
Estatística
-
- Combinatória-analise combinatoria
por heloisacarvalho83 » Seg Fev 27, 2012 22:40
- 1 Respostas
- 2886 Exibições
- Última mensagem por Livia000

Qua Mai 23, 2012 00:26
Estatística
-
- combinatória
por Adilson » Sex Ago 28, 2009 13:50
- 1 Respostas
- 2139 Exibições
- Última mensagem por Molina

Sex Ago 28, 2009 21:19
Estatística
-
- Combinatória
por 2137RF » Sex Out 09, 2009 11:25
- 4 Respostas
- 3473 Exibições
- Última mensagem por shirata

Qui Nov 26, 2009 06:38
Estatística
-
- combinatória
por apoliveirarj » Dom Jul 25, 2010 16:50
- 2 Respostas
- 4876 Exibições
- Última mensagem por apoliveirarj

Qui Ago 05, 2010 19:27
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Proporcionalidade
Autor:
silvia fillet - Qui Out 13, 2011 22:46
Divida o numero 35 em partes diretamente proporcionais a 4, 10 e 14. Em seguida divida o mesmo numero em partes proporcionais a 6, 15 e 21. explique por que os resultados sao iguais.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Sáb Out 15, 2011 10:25
POR GENTILEZA PODEM VERIFICAR SE O MEU RACIOCINIO ESTÁ CERTO?
P1 = K.4 SUBSTITUINDO K POR 1,25 P1= 5
P2 = K.10 SUBSTITUINDO K POR 1,25 P2= 12,50
P3 = K.13 SUBSTITUINDO K POR 1,25 P3= 17,50
P1+P2+P3 = 35
K.4+K.10+K.13 = 35
28 K = 35
K= 1,25
P1 = K.6 SUBSTITUINDO K POR 0,835 P1= 5
P2 = K.15 SUBSTITUINDO K POR 0,835 P2 = 12,50
P3 = K.21 SUBSTITUINDO K POR 0,835 P3 = 17,50
K.6+K.15+K.21 = 35
42K = 35
K= 0,833
4/6 =10/15 =14/21 RAZÃO = 2/3
SERÁ QUE ESTÁ CERTO?
ALGUEM PODE ME AJUDAR A EXPLICAR MELHOR?
OBRIGADA
SILVIA
Assunto:
Proporcionalidade
Autor:
ivanfx - Dom Out 16, 2011 00:37
utilize a definição e não se baseie no exercícios resolvidos da redefor, assim você terá mais clareza, mas acredito que sua conclusão esteja correto, pois o motivo de darem o mesmo resultado é pq a razão é a mesma.
Assunto:
Proporcionalidade
Autor:
Marcos Roberto - Dom Out 16, 2011 18:24
Silvia:
Acho que o resultado é o mesmo pq as razões dos coeficientes e as razões entre os números são inversamente proporcionais.
Você conseguiu achar o dia em que caiu 15 de novembro de 1889?
Assunto:
Proporcionalidade
Autor:
deiasp - Dom Out 16, 2011 23:45
Ola pessoal
Tb. estou no redefor
O dia da semana em 15 de novembro de 1889, acredito que foi em uma sexta feira
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 06:23
Bom dia,
Realmente foi uma sexta feira, como fazer os calculos para chegar ?
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 07:18
Para encontrar o dia que caiu 15 de novembro de 1889 você deve em primeiro lugar encontrar a quantidade de anos bissextos que houve entre 1889 à 2011, após isso dá uma verificada no ano 1900, ele não é bissexto, pois a regra diz que ano que é múltiplo de 100 e não é múltiplo de 400 não é bissexto.
Depois calcule quantos dias dão de 1889 até 2011, basta pegar a quantidade de anos e multiplicar por 365 + 1 dia a cada ano bissexto (esse resultado você calculou quando encontrou a quantidade de anos bissextos)
Pegue o resultado e divida por 7 e vai obter o resto.
obtendo o resto e partindo da data que pegou como referência conte a quantidade do resto para trás da semana.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 07:40
Bom dia,
Será que é assim:
2011 a 1889 são 121 anos sendo , 30 anos bissextos e 91 anos normais então temos:
30x366 = 10.980 dias
91x365 = 33.215 dias
incluindo 15/11/1889 - 31/12/1889 47 dias
33215+10980+47 = 44242 dias
44242:7 = 6320 + resto 2
è assim, nâo sei mais sair disso.
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 10:24
que tal descontar 1 dia do seu resultado, pois 1900 não é bissexto, ai seria 44241 e quando fizer a divisão o resto será 1
como etá pegando base 1/01/2011, se reparar bem 01/01/2011 sempre cai no mesmo dia que 15/01/2011, sendo assim se 01/01/2011 caiu em um sábado volte 1 dia para trás, ou seja, você está no sábado e voltando 1 dia voltará para sexta.então 15/11/1889 cairá em uma sexta
Assunto:
Proporcionalidade
Autor:
Kiwamen2903 - Seg Out 17, 2011 19:43
Boa noite, sou novo por aqui, espero poder aprender e ajudar quando possível! A minha resposta ficou assim:
De 1889 até 2001 temos 29 anos bissextos a começar por 1892 (primeiro múltiplo de 4 após 1889) e terminar por 2008 (último múltiplo de 4 antes de 2011). Vale lembrar que o ano 1900 não é bissexto, uma vez que é múltiplo de 100 mas não é múltiplo de 400.
De um ano normal para outro, se considerarmos a mesma data, eles caem em dias consecutivos da semana. Por exemplo 01/01/2011 – sábado, e 01/01/2010 – sexta.
De um ano bissexto para outro, se considerarmos a mesma data, um cai dois dias da semana depois do outro. Por exemplo 01/01/2008 (ano bissexto) – Terça – feira, e 01/01/09 – Quinta-feira.
Sendo assim, se contarmos um dia da semana de diferença para cada um dos 01/01 dos 122 anos que separam 1889 e 2011 mais os 29 dias a mais referentes aos anos bissextos entre 1889 e 2011, concluímos que são 151 dias da semana de diferença, o que na realidade nos trás: 151:7= 21x7+4, isto é, são 4 dias da semana de diferença. Logo, como 15/11/2011 cairá em uma terça-feira, 15/11/1889 caiu em uma sexta-feira.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






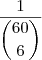 , assim, fazendo
, assim, fazendo 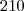 jogos distintos, as chances aumentam para
jogos distintos, as chances aumentam para 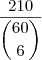 .
.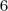 números dentre os
números dentre os  escolhidos como
escolhidos como 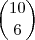 , assim suas chances são de
, assim suas chances são de 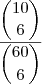 .
.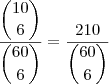 , independendo do método que você escolher, suas chances são as mesmas. Acho que por isso do valor já ser de
, independendo do método que você escolher, suas chances são as mesmas. Acho que por isso do valor já ser de  reais.
reais. 

, assim, fazendo
jogos distintos, as chances aumentam para
.
números dentre os
escolhidos como
, assim suas chances são de
.
, independendo do método que você escolher, suas chances são as mesmas. Acho que por isso do valor já ser de
reais.
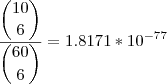
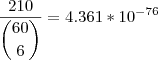

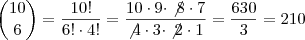
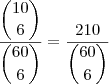 .
.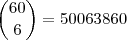
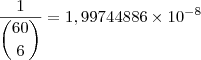
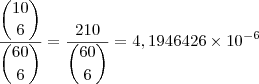
.
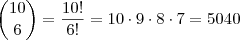
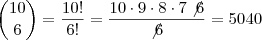
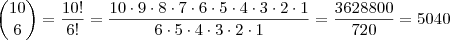

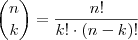 , por isso da diferença entre as soluções.
, por isso da diferença entre as soluções. apostas separadamente.
apostas separadamente. 
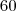 números numa só cartela. Pelo que já foi visto nesse tópico, o preço seria de
números numa só cartela. Pelo que já foi visto nesse tópico, o preço seria de 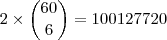 reais. Fica a dica: da próxima vez que a Mega Sena acumulada ultrapassar este valor, aposte e torça para ganhar o prêmio sozinho.
reais. Fica a dica: da próxima vez que a Mega Sena acumulada ultrapassar este valor, aposte e torça para ganhar o prêmio sozinho. 





