


aspirantestudante escreveu:Sabe-se que -2 e 3 são raízes de uma função quadrática. Se o ponto (-1 , 8) pertence ao gráfico dessa função, então:
(1) [ ] o seu valor máximo é 1,25
(2) [ ] o seu valor mínimo é 1,25
(3) [ ] o seu valor máximo é 0,25
(4) [ ] o seu valor mínimo é 12,5
(5) [ ] o seu valor máximo é 12,5.



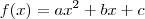 , logo:
, logo: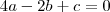





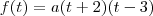 . Conhecendo o outro ponto:
. Conhecendo o outro ponto:  . Logo, boca para baixo e a parábola tem um máximo que é na soma das raízes (
. Logo, boca para baixo e a parábola tem um máximo que é na soma das raízes ( 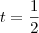 ) . Jogando na função:
) . Jogando na função: 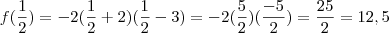 .
.

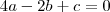

 Vamos colocar essa linha para cima.
Vamos colocar essa linha para cima.

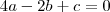 agora jogar para matrizes.
agora jogar para matrizes.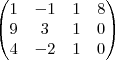 aplica chió acho que voce deve saber e irá gerar isso:
aplica chió acho que voce deve saber e irá gerar isso: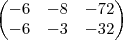 volta para sistema.
volta para sistema.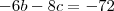
 desse jeito irá achar os valores de a,b,c.
desse jeito irá achar os valores de a,b,c.

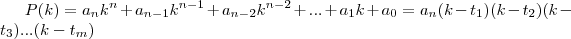
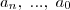 são constantes e
são constantes e  são as raízes.
são as raízes.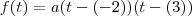
 para encontrar o valor da constante. Como deu negativo, sabemos que a parábola tem boca para baixo, e portanto tem um ponto de máximo. Pela simetria da parábola, o ponto de máximo é a média aritmética das raízes no eixo das abcissas (que é chamado a abcissa do vértice) e a ordenada é
para encontrar o valor da constante. Como deu negativo, sabemos que a parábola tem boca para baixo, e portanto tem um ponto de máximo. Pela simetria da parábola, o ponto de máximo é a média aritmética das raízes no eixo das abcissas (que é chamado a abcissa do vértice) e a ordenada é 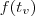 .
.



 é um porque, embora as raízes sejam as mesmas, não quer dizer que a função passe pelo ponto
é um porque, embora as raízes sejam as mesmas, não quer dizer que a função passe pelo ponto  , condição dada pelo exercício. Existem infinitas funções quadráticas que tem as mesmas raízes, porém só existe uma que, além dessas raízes, passa pelo ponto dado no exercício.
, condição dada pelo exercício. Existem infinitas funções quadráticas que tem as mesmas raízes, porém só existe uma que, além dessas raízes, passa pelo ponto dado no exercício.




Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
