 por Cleyson007 » Ter Jul 01, 2008 01:43
por Cleyson007 » Ter Jul 01, 2008 01:43
Olá, Fábio, tudo bem?
Estudando um pouco de matemática, deparei-me com uma questão bem assim:
O valor da expressão
![\sqrt[3]{\frac{{2}^{28}+{2}^{30}}{10}} \sqrt[3]{\frac{{2}^{28}+{2}^{30}}{10}}](/latexrender/pictures/b709a448b39c7dc6872fb04edbc002f2.png)
é?
Eu a resolvi da seguinte maneira:
![\sqrt[3]{\frac{{2}^{0}+{{2}^{{i}^{2}}}^{}}{10}}\Rightarrow
\sqrt[3]{\frac{1-2}{10}}\Rightarrow
\sqrt[3]{\frac{-1}{10}}\Rightarrow
\frac{\sqrt[3]{-1}}{\sqrt[3]{10}} \sqrt[3]{\frac{{2}^{0}+{{2}^{{i}^{2}}}^{}}{10}}\Rightarrow
\sqrt[3]{\frac{1-2}{10}}\Rightarrow
\sqrt[3]{\frac{-1}{10}}\Rightarrow
\frac{\sqrt[3]{-1}}{\sqrt[3]{10}}](/latexrender/pictures/980a31b7cf0ef06939922d0381c01ecb.png)
Está correta a resolução do problema?
Desde já agradeço!
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por admin » Ter Jul 01, 2008 07:10
por admin » Ter Jul 01, 2008 07:10
Olá, Cleyson!
As primeiras perguntas que fiz para avaliar a expressão foram:
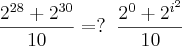
Ou seja:
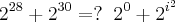
Ou ainda:

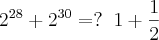

Pense nelas!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Cleyson007 » Ter Jul 01, 2008 11:27
por Cleyson007 » Ter Jul 01, 2008 11:27
Eu tentei resolvê-la por números complexos: 1) Onde

já que 28/4= 7 e resta zero (0). Todo número elevado a zero (0) = 1; ou seja: {2}^{0}=1

. Eu cometi um vacilo e coloquei -2 sendo que era

Então, ficaria assim o problema apresentado?
![\sqrt[3]{\frac{1+{2}^{-1}}{10}}\Rightarrow\sqrt[3]{\frac{\frac{3}{2}}{10}}\Rightarrow\sqrt[3]{\frac{3}{20}}} \sqrt[3]{\frac{1+{2}^{-1}}{10}}\Rightarrow\sqrt[3]{\frac{\frac{3}{2}}{10}}\Rightarrow\sqrt[3]{\frac{3}{20}}}](/latexrender/pictures/08ef1c0837e760f811e14c221780dc54.png)
O meu modo de resolver está correto? Ajude-me por favor!
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por admin » Ter Jul 01, 2008 12:04
por admin » Ter Jul 01, 2008 12:04
Bom dia!
Não Cleyson, não pode ser.
Você pensou nas perguntas?
Veja que este número é bem grande:
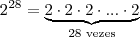
Ele não pode ser igual a um! Concorda?
Este outro é maior ainda!

Não pode ser igual a meio!
Cleyson007 escreveu:Eu tentei resolvê-la por números complexos: 1) Onde

já que 28/4= 7 e resta zero (0).
Cleyson, esta afirmação que você fez não é verdade.
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por PIMENTA » Sáb Jul 05, 2008 21:41
por PIMENTA » Sáb Jul 05, 2008 21:41
Por não ter muita habilidade com a escrita gráfica em computador, formularei uma resposta por escrito, na forma gramatical, sem ater-me em gráficos.
o problema proposto é calcular a raiz cúbica de 2 elevado a 28 mais dois elevado a 30, dividido por 10. Aplicando o produto de uma potência por uma soma podemos reescrever a expressão na forma de raiz cúbica de 2 elevado ao quadrado vezes a soma de 2 elevado a 14 mais 2 elevado a 15, dividido por 10, já que 2x14=28 e 2x15=30, para 2 elevado a 15 podemos escrever 2 x 2 elevado a 14. Fatorando a expressão, teremos raiz cúbica de 2 elevado a 2 x 2 elevado a 14, fora do parênteses e 1 + 2 dentro do parênteses, daí fazendo as contas teremos como resultado final 32 vezes raiz cúbica de 3/5.
-
PIMENTA
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sáb Jul 05, 2008 13:24
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: direito
- Andamento: formado
 por admin » Dom Jul 06, 2008 11:14
por admin » Dom Jul 06, 2008 11:14
Olá
PIMENTA!
Sobre escrever as expressões matemáticas, você pode utilizar o botão "Editor de Fórmulas", enquanto se acostuma com a linguagem LaTeX.
Na janela que se abrirá, há botões para prever a expressão e inserir na mensagem.
Também, parando o ponteiro do mouse sobre o gráfico, a expressão utilizada é exibida.
Há um erro em sua primeira passagem:
No produto de potências de mesma base, devemos somar os expoentes, e não multiplicar. Assim como você fez nas demais passagens.
PIMENTA escreveu:![\sqrt[3]{\frac{{2}^{28}+{2}^{30}}{10}} =
\xcancel{ \sqrt[3]{\frac{ 2^2 \left({2}^{14}+{2}^{15} \right) }{10}} } =
\sqrt[3]{\frac{ 2^2 \left({2}^{14}+2\cdot{2}^{14} \right) }{10}} =
\sqrt[3]{\frac{ 2^2\cdot 2^{14} \left(1+2 \right) }{10}} = \sqrt[3]{\frac{{2}^{28}+{2}^{30}}{10}} =
\xcancel{ \sqrt[3]{\frac{ 2^2 \left({2}^{14}+{2}^{15} \right) }{10}} } =
\sqrt[3]{\frac{ 2^2 \left({2}^{14}+2\cdot{2}^{14} \right) }{10}} =
\sqrt[3]{\frac{ 2^2\cdot 2^{14} \left(1+2 \right) }{10}} =](/latexrender/pictures/0ce5d96716d36433fd461935b0d6535f.png)
![= \sqrt[3]{\frac{ 2^{16} \cdot 3}{2\cdot 5}} =
\sqrt[3]{2^{15} \cdot \frac{3}{5}} =
2^{5}\cdot\sqrt[3]{\frac{3}{5}} =
32\cdot\sqrt[3]{\frac{3}{5}} = \sqrt[3]{\frac{ 2^{16} \cdot 3}{2\cdot 5}} =
\sqrt[3]{2^{15} \cdot \frac{3}{5}} =
2^{5}\cdot\sqrt[3]{\frac{3}{5}} =
32\cdot\sqrt[3]{\frac{3}{5}}](/latexrender/pictures/e802cb9c0bba3cdd5281aa9594c1cd1d.png)
Veja que fazendo a distributiva, a expressão resultante é diferente da inicial:
![\sqrt[3]{\frac{ 2^2 \left({2}^{14}+{2}^{15} \right) }{10}} =
\sqrt[3]{\frac{ {2}^{16}+{2}^{17} }{10}} \neq
\sqrt[3]{\frac{{2}^{28}+{2}^{30}}{10}} \sqrt[3]{\frac{ 2^2 \left({2}^{14}+{2}^{15} \right) }{10}} =
\sqrt[3]{\frac{ {2}^{16}+{2}^{17} }{10}} \neq
\sqrt[3]{\frac{{2}^{28}+{2}^{30}}{10}}](/latexrender/pictures/c6c0502a00ddb7abbee09395d36aae8b.png)
Portanto,
![\sqrt[3]{\frac{{2}^{28}+{2}^{30}}{10}}
\neq
32\cdot\sqrt[3]{\frac{3}{5}} \sqrt[3]{\frac{{2}^{28}+{2}^{30}}{10}}
\neq
32\cdot\sqrt[3]{\frac{3}{5}}](/latexrender/pictures/5d0837330c07d6f799cc7b1d30ecab6f.png)
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por admin » Dom Jul 06, 2008 18:11
por admin » Dom Jul 06, 2008 18:11
Olá Cleyson!
Vou escrever as passagens em detalhes, por favor comente:
![\sqrt[3]{\frac{2^{28}+2^{30}}{10}} =
\sqrt[3]{\frac{2^{14+14}+2^{14+14+2}}{10}} =
\sqrt[3]{\frac{2^{14}\cdot 2^{14}+2^{14}\cdot 2^{14}\cdot 2^2}{10}} =
\sqrt[3]{\frac{2^{14}\cdot 2^{14}\left( 1 + 1\cdot 2^2 \right)}{10}} = \sqrt[3]{\frac{2^{28}+2^{30}}{10}} =
\sqrt[3]{\frac{2^{14+14}+2^{14+14+2}}{10}} =
\sqrt[3]{\frac{2^{14}\cdot 2^{14}+2^{14}\cdot 2^{14}\cdot 2^2}{10}} =
\sqrt[3]{\frac{2^{14}\cdot 2^{14}\left( 1 + 1\cdot 2^2 \right)}{10}} =](/latexrender/pictures/88917fa6fcd13e90b7a25a06521c930c.png)
![= \sqrt[3]{\frac{2^{14+14} \left( 1 + 4\right)}{2\cdot 5}} =
\sqrt[3]{\frac{2^{28} \cdot 5}{2\cdot 5}} =
\sqrt[3]{\frac{2^{28}}{2^1} \cdot \frac{5}{5}} = = \sqrt[3]{\frac{2^{14+14} \left( 1 + 4\right)}{2\cdot 5}} =
\sqrt[3]{\frac{2^{28} \cdot 5}{2\cdot 5}} =
\sqrt[3]{\frac{2^{28}}{2^1} \cdot \frac{5}{5}} =](/latexrender/pictures/ff340bbdf8efa4ea101e078e97f1d24b.png)
![= \sqrt[3]{2^{28-1} \cdot 1} =
\sqrt[3]{2^{27}} =
2^{\frac{27}{3}} =
2^9 = 512 = \sqrt[3]{2^{28-1} \cdot 1} =
\sqrt[3]{2^{27}} =
2^{\frac{27}{3}} =
2^9 = 512](/latexrender/pictures/a3ebd74eb4af0376a1591aa8dfc7d473.png)
Até mais!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por PIMENTA » Ter Jul 08, 2008 00:58
por PIMENTA » Ter Jul 08, 2008 00:58
Olá Professor, realmente, houve um deslize por minha parte quando escrevi o produto de potências. Da próxima vez estarei mais atento quanto às propriedades operatórias das potências. Não sou formado em matemática, apesar ter iniciado o curso por duas vezes na Universidade Federal de Goiás - UFG, onde fiz apenas algumas matérias, tais como: Matemática I, maemática II, Probabilidade e Estatistica, Cálculo I, Geometria Plana, Geometria Analítica e Fundamentos da Física Clássica.
Hoje sou formado em direito, mas gosto muito de matemática. Perdoe-me as minhas intromissões indevidas.
-
PIMENTA
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sáb Jul 05, 2008 13:24
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: direito
- Andamento: formado
 por admin » Qui Jul 17, 2008 01:52
por admin » Qui Jul 17, 2008 01:52
Olá Pimenta!
Seu pedido de perdão é desnecessário, todas as participações são bem-vindas.
Até mais.
Um abraço!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por paulo testoni » Qua Out 01, 2008 16:23
por paulo testoni » Qua Out 01, 2008 16:23
Hola Cleyson007.
Aqui devemos usar as propriedades das potências, veja:
![\sqrt[3]{\frac{{2}^{28}+{2}^{30}}{10}} \sqrt[3]{\frac{{2}^{28}+{2}^{30}}{10}}](/latexrender/pictures/b709a448b39c7dc6872fb04edbc002f2.png)
![\sqrt[3]{\frac{{2}^{27}*{2}^1+{2}^{27}*{2}^3}{10}} \sqrt[3]{\frac{{2}^{27}*{2}^1+{2}^{27}*{2}^3}{10}}](/latexrender/pictures/e03d728b331096ca3c5155a6512aa428.png)
, agora coloque
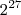
em evidência dentro da raiz cúbica, assim:
![\sqrt[3]{\frac{{2}^{27}*[{2}^1+{2}^3]}{10}} \sqrt[3]{\frac{{2}^{27}*[{2}^1+{2}^3]}{10}}](/latexrender/pictures/21c85b30f08d1d69dceae4c73f6c11c4.png)
,
![\sqrt[3]{\frac{{2}^{27}*[2+8]}{10}} \sqrt[3]{\frac{{2}^{27}*[2+8]}{10}}](/latexrender/pictures/e2e11826f70ad8a71337729f4eda5763.png)
,
![\sqrt[3]{\frac{{2}^{27}*10}{10}} \sqrt[3]{\frac{{2}^{27}*10}{10}}](/latexrender/pictures/6668be0dd4b15b852bd4b099788b9976.png)
, corte o 10, fica:
![\sqrt[3]{2^{27}} \sqrt[3]{2^{27}}](/latexrender/pictures/7983d4b8f46f5ff41beefdf21e366e3f.png)
, divida 27 pelo índice da raiz, temos:

. Creio que é isso.
-
paulo testoni
- Usuário Dedicado

-
- Mensagens: 45
- Registrado em: Ter Set 30, 2008 11:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Expressoes
por Biinha » Ter Fev 19, 2013 16:55
- 4 Respostas
- 2436 Exibições
- Última mensagem por Biinha

Sex Fev 22, 2013 11:41
Conjuntos
-
- expressoes
 por Bernardo Silva » Sáb Nov 19, 2016 16:40
por Bernardo Silva » Sáb Nov 19, 2016 16:40
- 1 Respostas
- 1622 Exibições
- Última mensagem por Jadiel Carlos

Seg Nov 21, 2016 11:54
Cálculo: Limites, Derivadas e Integrais
-
- [expressões] ajuda
por kaic » Seg Abr 07, 2008 23:48
- 5 Respostas
- 3976 Exibições
- Última mensagem por admin

Ter Abr 08, 2008 05:04
Álgebra Elementar
-
- Cálculo de Expressões
por Jansen » Dom Ago 30, 2009 01:28
- 2 Respostas
- 2817 Exibições
- Última mensagem por Jansen

Dom Ago 30, 2009 17:17
Sistemas de Equações
-
- Simplicando expressões
por Florisbela » Dom Mai 23, 2010 19:48
- 1 Respostas
- 1444 Exibições
- Última mensagem por DanielFerreira

Ter Jun 08, 2010 18:38
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[3]{\frac{{2}^{28}+{2}^{30}}{10}} \sqrt[3]{\frac{{2}^{28}+{2}^{30}}{10}}](/latexrender/pictures/b709a448b39c7dc6872fb04edbc002f2.png) é?
é?![\sqrt[3]{\frac{{2}^{0}+{{2}^{{i}^{2}}}^{}}{10}}\Rightarrow
\sqrt[3]{\frac{1-2}{10}}\Rightarrow
\sqrt[3]{\frac{-1}{10}}\Rightarrow
\frac{\sqrt[3]{-1}}{\sqrt[3]{10}} \sqrt[3]{\frac{{2}^{0}+{{2}^{{i}^{2}}}^{}}{10}}\Rightarrow
\sqrt[3]{\frac{1-2}{10}}\Rightarrow
\sqrt[3]{\frac{-1}{10}}\Rightarrow
\frac{\sqrt[3]{-1}}{\sqrt[3]{10}}](/latexrender/pictures/980a31b7cf0ef06939922d0381c01ecb.png)

![\sqrt[3]{\frac{{2}^{28}+{2}^{30}}{10}} \sqrt[3]{\frac{{2}^{28}+{2}^{30}}{10}}](/latexrender/pictures/b709a448b39c7dc6872fb04edbc002f2.png) é?
é?![\sqrt[3]{\frac{{2}^{0}+{{2}^{{i}^{2}}}^{}}{10}}\Rightarrow
\sqrt[3]{\frac{1-2}{10}}\Rightarrow
\sqrt[3]{\frac{-1}{10}}\Rightarrow
\frac{\sqrt[3]{-1}}{\sqrt[3]{10}} \sqrt[3]{\frac{{2}^{0}+{{2}^{{i}^{2}}}^{}}{10}}\Rightarrow
\sqrt[3]{\frac{1-2}{10}}\Rightarrow
\sqrt[3]{\frac{-1}{10}}\Rightarrow
\frac{\sqrt[3]{-1}}{\sqrt[3]{10}}](/latexrender/pictures/980a31b7cf0ef06939922d0381c01ecb.png)

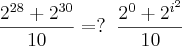
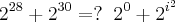

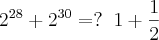


 já que 28/4= 7 e resta zero (0). Todo número elevado a zero (0) = 1; ou seja: {2}^{0}=1
já que 28/4= 7 e resta zero (0). Todo número elevado a zero (0) = 1; ou seja: {2}^{0}=1 . Eu cometi um vacilo e coloquei -2 sendo que era
. Eu cometi um vacilo e coloquei -2 sendo que era 
![\sqrt[3]{\frac{1+{2}^{-1}}{10}}\Rightarrow\sqrt[3]{\frac{\frac{3}{2}}{10}}\Rightarrow\sqrt[3]{\frac{3}{20}}} \sqrt[3]{\frac{1+{2}^{-1}}{10}}\Rightarrow\sqrt[3]{\frac{\frac{3}{2}}{10}}\Rightarrow\sqrt[3]{\frac{3}{20}}}](/latexrender/pictures/08ef1c0837e760f811e14c221780dc54.png)

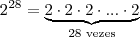

já que 28/4= 7 e resta zero (0).


![\sqrt[3]{\frac{ 2^2 \left({2}^{14}+{2}^{15} \right) }{10}} =
\sqrt[3]{\frac{ {2}^{16}+{2}^{17} }{10}} \neq
\sqrt[3]{\frac{{2}^{28}+{2}^{30}}{10}} \sqrt[3]{\frac{ 2^2 \left({2}^{14}+{2}^{15} \right) }{10}} =
\sqrt[3]{\frac{ {2}^{16}+{2}^{17} }{10}} \neq
\sqrt[3]{\frac{{2}^{28}+{2}^{30}}{10}}](/latexrender/pictures/c6c0502a00ddb7abbee09395d36aae8b.png)
![\sqrt[3]{\frac{{2}^{28}+{2}^{30}}{10}}
\neq
32\cdot\sqrt[3]{\frac{3}{5}} \sqrt[3]{\frac{{2}^{28}+{2}^{30}}{10}}
\neq
32\cdot\sqrt[3]{\frac{3}{5}}](/latexrender/pictures/5d0837330c07d6f799cc7b1d30ecab6f.png)

![\sqrt[3]{\frac{2^{28}+2^{30}}{10}} =
\sqrt[3]{\frac{2^{14+14}+2^{14+14+2}}{10}} =
\sqrt[3]{\frac{2^{14}\cdot 2^{14}+2^{14}\cdot 2^{14}\cdot 2^2}{10}} =
\sqrt[3]{\frac{2^{14}\cdot 2^{14}\left( 1 + 1\cdot 2^2 \right)}{10}} = \sqrt[3]{\frac{2^{28}+2^{30}}{10}} =
\sqrt[3]{\frac{2^{14+14}+2^{14+14+2}}{10}} =
\sqrt[3]{\frac{2^{14}\cdot 2^{14}+2^{14}\cdot 2^{14}\cdot 2^2}{10}} =
\sqrt[3]{\frac{2^{14}\cdot 2^{14}\left( 1 + 1\cdot 2^2 \right)}{10}} =](/latexrender/pictures/88917fa6fcd13e90b7a25a06521c930c.png)
![= \sqrt[3]{\frac{2^{14+14} \left( 1 + 4\right)}{2\cdot 5}} =
\sqrt[3]{\frac{2^{28} \cdot 5}{2\cdot 5}} =
\sqrt[3]{\frac{2^{28}}{2^1} \cdot \frac{5}{5}} = = \sqrt[3]{\frac{2^{14+14} \left( 1 + 4\right)}{2\cdot 5}} =
\sqrt[3]{\frac{2^{28} \cdot 5}{2\cdot 5}} =
\sqrt[3]{\frac{2^{28}}{2^1} \cdot \frac{5}{5}} =](/latexrender/pictures/ff340bbdf8efa4ea101e078e97f1d24b.png)
![= \sqrt[3]{2^{28-1} \cdot 1} =
\sqrt[3]{2^{27}} =
2^{\frac{27}{3}} =
2^9 = 512 = \sqrt[3]{2^{28-1} \cdot 1} =
\sqrt[3]{2^{27}} =
2^{\frac{27}{3}} =
2^9 = 512](/latexrender/pictures/a3ebd74eb4af0376a1591aa8dfc7d473.png)



![\sqrt[3]{\frac{{2}^{28}+{2}^{30}}{10}} \sqrt[3]{\frac{{2}^{28}+{2}^{30}}{10}}](/latexrender/pictures/b709a448b39c7dc6872fb04edbc002f2.png)
![\sqrt[3]{\frac{{2}^{27}*{2}^1+{2}^{27}*{2}^3}{10}} \sqrt[3]{\frac{{2}^{27}*{2}^1+{2}^{27}*{2}^3}{10}}](/latexrender/pictures/e03d728b331096ca3c5155a6512aa428.png) , agora coloque
, agora coloque 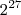 em evidência dentro da raiz cúbica, assim:
em evidência dentro da raiz cúbica, assim:![\sqrt[3]{\frac{{2}^{27}*[{2}^1+{2}^3]}{10}} \sqrt[3]{\frac{{2}^{27}*[{2}^1+{2}^3]}{10}}](/latexrender/pictures/21c85b30f08d1d69dceae4c73f6c11c4.png) ,
,![\sqrt[3]{\frac{{2}^{27}*[2+8]}{10}} \sqrt[3]{\frac{{2}^{27}*[2+8]}{10}}](/latexrender/pictures/e2e11826f70ad8a71337729f4eda5763.png) ,
,![\sqrt[3]{\frac{{2}^{27}*10}{10}} \sqrt[3]{\frac{{2}^{27}*10}{10}}](/latexrender/pictures/6668be0dd4b15b852bd4b099788b9976.png) , corte o 10, fica:
, corte o 10, fica:![\sqrt[3]{2^{27}} \sqrt[3]{2^{27}}](/latexrender/pictures/7983d4b8f46f5ff41beefdf21e366e3f.png) , divida 27 pelo índice da raiz, temos:
, divida 27 pelo índice da raiz, temos: . Creio que é isso.
. Creio que é isso.
 } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: } você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais? } você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?