[expressões] problema

por **Cleyson007** » Ter Jul 01, 2008 01:43

Olá, Fábio, tudo bem?
Estudando um pouco de matemática, deparei-me com uma questão bem assim:
O valor da expressão $\sqrt[3]{\frac{{2}^{28}+{2}^{30}}{10}}$ é?
Eu a resolvi da seguinte maneira:
$\sqrt[3]{\frac{{2}^{0}+{{2}^{{i}^{2}}}^{}}{10}}\Rightarrow \sqrt[3]{\frac{1-2}{10}}\Rightarrow \sqrt[3]{\frac{-1}{10}}\Rightarrow \frac{\sqrt[3]{-1}}{\sqrt[3]{10}}$
Está correta a resolução do problema?
Desde já agradeço!

por **admin** » Ter Jul 01, 2008 07:10

Olá, Cleyson!

As primeiras perguntas que fiz para avaliar a expressão foram:
$\frac{2^{28}+2^{30}}{10} =? \;\; \frac{2^0+{2^{i^2}}}{10}$

Ou seja:
$2^{28}+2^{30} =? \;\; 2^0+{2^{i^2}}$

Ou ainda:
$2^{28}+2^{30} =? \;\; 1+2^{-1}$

$2^{28}+2^{30} =? \;\; 1+\frac12$

$2^{28}+2^{30} =? \;\; \frac32$

Pense nelas!

por **Cleyson007** » Ter Jul 01, 2008 11:27

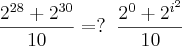
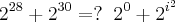
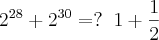
Eu tentei resolvê-la por números complexos: 1) Onde ${2}^{28}= {2}^{0}$ já que 28/4= 7 e resta zero (0). Todo número elevado a zero (0) = 1; ou seja: {2}^{0}=1

. Eu cometi um vacilo e coloquei -2 sendo que era ${2}^{-1}$
Então, ficaria assim o problema apresentado? $\sqrt[3]{\frac{1+{2}^{-1}}{10}}\Rightarrow\sqrt[3]{\frac{\frac{3}{2}}{10}}\Rightarrow\sqrt[3]{\frac{3}{20}}}$
O meu modo de resolver está correto? Ajude-me por favor!

por **admin** » Ter Jul 01, 2008 12:04

Bom dia!

Não Cleyson, não pode ser.
Você pensou nas perguntas?

Veja que este número é bem grande:
$2^{28} = \underbrace{2 \cdot 2 \cdot 2 \cdot ... \cdot 2}_{\text{28 vezes}}$
Ele não pode ser igual a um! Concorda?

Este outro é maior ainda!
$2^{30} = \underbrace{2 \cdot 2 \cdot 2 \cdot ... \cdot 2}_{\text{30 vezes}}$
Não pode ser igual a meio!

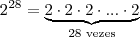
Cleyson007 escreveu:Eu tentei resolvê-la por números complexos: 1) Onde ${2}^{28}= {2}^{0}$ já que 28/4= 7 e resta zero (0).

Cleyson, esta afirmação que você fez não é verdade.

por **PIMENTA** » Sáb Jul 05, 2008 21:41

Por não ter muita habilidade com a escrita gráfica em computador, formularei uma resposta por escrito, na forma gramatical, sem ater-me em gráficos.
o problema proposto é calcular a raiz cúbica de 2 elevado a 28 mais dois elevado a 30, dividido por 10. Aplicando o produto de uma potência por uma soma podemos reescrever a expressão na forma de raiz cúbica de 2 elevado ao quadrado vezes a soma de 2 elevado a 14 mais 2 elevado a 15, dividido por 10, já que 2x14=28 e 2x15=30, para 2 elevado a 15 podemos escrever 2 x 2 elevado a 14. Fatorando a expressão, teremos raiz cúbica de 2 elevado a 2 x 2 elevado a 14, fora do parênteses e 1 + 2 dentro do parênteses, daí fazendo as contas teremos como resultado final 32 vezes raiz cúbica de 3/5.

por **admin** » Dom Jul 06, 2008 11:14

Olá PIMENTA!

Sobre escrever as expressões matemáticas, você pode utilizar o botão "Editor de Fórmulas", enquanto se acostuma com a linguagem LaTeX.
Na janela que se abrirá, há botões para prever a expressão e inserir na mensagem.
Também, parando o ponteiro do mouse sobre o gráfico, a expressão utilizada é exibida.

Há um erro em sua primeira passagem:
No produto de potências de mesma base, devemos somar os expoentes, e não multiplicar. Assim como você fez nas demais passagens.

PIMENTA escreveu:
$\sqrt[3]{\frac{{2}^{28}+{2}^{30}}{10}} = \xcancel{ \sqrt[3]{\frac{ 2^2 \left({2}^{14}+{2}^{15} \right) }{10}} } = \sqrt[3]{\frac{ 2^2 \left({2}^{14}+2\cdot{2}^{14} \right) }{10}} = \sqrt[3]{\frac{ 2^2\cdot 2^{14} \left(1+2 \right) }{10}} =$

$= \sqrt[3]{\frac{ 2^{16} \cdot 3}{2\cdot 5}} = \sqrt[3]{2^{15} \cdot \frac{3}{5}} = 2^{5}\cdot\sqrt[3]{\frac{3}{5}} = 32\cdot\sqrt[3]{\frac{3}{5}}$

Veja que fazendo a distributiva, a expressão resultante é diferente da inicial:

$\sqrt[3]{\frac{ 2^2 \left({2}^{14}+{2}^{15} \right) }{10}} = \sqrt[3]{\frac{ {2}^{16}+{2}^{17} }{10}} \neq \sqrt[3]{\frac{{2}^{28}+{2}^{30}}{10}}$

Portanto,

$\sqrt[3]{\frac{{2}^{28}+{2}^{30}}{10}} \neq 32\cdot\sqrt[3]{\frac{3}{5}}$

por **admin** » Dom Jul 06, 2008 18:11

Olá Cleyson!

Vou escrever as passagens em detalhes, por favor comente:

$\sqrt[3]{\frac{2^{28}+2^{30}}{10}} = \sqrt[3]{\frac{2^{14+14}+2^{14+14+2}}{10}} = \sqrt[3]{\frac{2^{14}\cdot 2^{14}+2^{14}\cdot 2^{14}\cdot 2^2}{10}} = \sqrt[3]{\frac{2^{14}\cdot 2^{14}\left( 1 + 1\cdot 2^2 \right)}{10}} =$

$= \sqrt[3]{\frac{2^{14+14} \left( 1 + 4\right)}{2\cdot 5}} = \sqrt[3]{\frac{2^{28} \cdot 5}{2\cdot 5}} = \sqrt[3]{\frac{2^{28}}{2^1} \cdot \frac{5}{5}} =$

$= \sqrt[3]{2^{28-1} \cdot 1} = \sqrt[3]{2^{27}} = 2^{\frac{27}{3}} = 2^9 = 512$

Até mais!

por **PIMENTA** » Ter Jul 08, 2008 00:58

Olá Professor, realmente, houve um deslize por minha parte quando escrevi o produto de potências. Da próxima vez estarei mais atento quanto às propriedades operatórias das potências. Não sou formado em matemática, apesar ter iniciado o curso por duas vezes na Universidade Federal de Goiás - UFG, onde fiz apenas algumas matérias, tais como: Matemática I, maemática II, Probabilidade e Estatistica, Cálculo I, Geometria Plana, Geometria Analítica e Fundamentos da Física Clássica.
Hoje sou formado em direito, mas gosto muito de matemática. Perdoe-me as minhas intromissões indevidas.

por **admin** » Qui Jul 17, 2008 01:52

Olá Pimenta!
Seu pedido de perdão é desnecessário, todas as participações são bem-vindas.

Até mais.
Um abraço!

por **paulo testoni** » Qua Out 01, 2008 16:23

Hola Cleyson007.

Aqui devemos usar as propriedades das potências, veja:

$\sqrt[3]{\frac{{2}^{28}+{2}^{30}}{10}}$

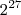$\sqrt[3]{\frac{{2}^{27}*{2}^1+{2}^{27}*{2}^3}{10}}$ , agora coloque $2^{27}$ em evidência dentro da raiz cúbica, assim:

$\sqrt[3]{\frac{{2}^{27}*[{2}^1+{2}^3]}{10}}$ ,

$\sqrt[3]{\frac{{2}^{27}*[2+8]}{10}}$ ,

$\sqrt[3]{\frac{{2}^{27}*10}{10}}$ , corte o 10, fica:

$\sqrt[3]{2^{27}}$ , divida 27 pelo índice da raiz, temos:

2^9 = 512

. Creio que é isso.

[expressões] problema

[expressões] problema

[expressões] problema

Re: problema

Re: problema

Re: problema

Re: problema

Re: problema

Re: problema

Re: problema

Re: problema

Re: [expressões] problema

Quem está online