Sistema com as ultimas equações iguais

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

Sistema com as ultimas equações iguais

Regras do fórum
Responder

Sistema com as ultimas equações iguais

Mensagempor Bruhh » Qui Set 09, 2010 21:33

Oii, Boa Noite!

Recentemente abri o tópico do sitema de 15 equações com 15 incógnitas. Pois bem, depois de muito tentar consegui escalonar o sistema até que restassem as quatro últimas equações com quatro incógnitas. Mas não sei, se por fazer algo errado, as últimas equações ficaram exatamente iguais. Agora não sei o que fazer, já que seu eu escalonar uma com a outra vou zerar tudo e se tentar escalonar com as outras equações apareceram mais letras novamente. Abaixo o meu grande proglema (está no formato de uma matriz aumentada, onde cada número da coluna P é o resutado da sua respectiva equação):

Matriz- algebra linear.JPG
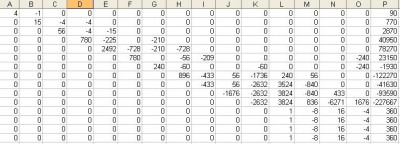
matriz



E agora o que eu faço? Como descobrir o valor de cada letra? E como fazer para ecalonar?

Muito Obrigada mais uma vez!
Bruhh
Usuário Dedicado
Usuário Dedicado
 
Mensagens: 47
Registrado em: Seg Mar 01, 2010 14:30
Formação Escolar: GRADUAÇÃO
Área/Curso: Bacharelado em Eng. Química
Andamento: cursando
Voltar ao topo

Re: Sistema com as ultimas equações iguais

Mensagempor MarceloFantini » Qui Set 09, 2010 22:13

Isso mostra que as 3 últimas equações do seu sistema são combinações lineares das outras, e portanto você tem um conjunto LD de vetores. Uma interpretação mais profunda disso depende de qual o significado do seu sistema.
Futuro MATEMÁTICO
e^{\pi \cdot i} +1 = 0
MarceloFantini
Colaborador Moderador
Colaborador Moderador
 
Mensagens: 3126
Registrado em: Seg Dez 14, 2009 11:41
Formação Escolar: GRADUAÇÃO
Andamento: formado
Voltar ao topo

Re: Sistema com as ultimas equações iguais

Mensagempor Bruhh » Sex Set 10, 2010 13:16

Mas tem alguma maneira de resolver isso? Ou escalonar?
Bruhh
Usuário Dedicado
Usuário Dedicado
 
Mensagens: 47
Registrado em: Seg Mar 01, 2010 14:30
Formação Escolar: GRADUAÇÃO
Área/Curso: Bacharelado em Eng. Química
Andamento: cursando
Voltar ao topo

Re: Sistema com as ultimas equações iguais

Mensagempor MarceloFantini » Sex Set 10, 2010 17:47

Isso mostra que o seu sistema não tem solução única.
Futuro MATEMÁTICO
e^{\pi \cdot i} +1 = 0
MarceloFantini
Colaborador Moderador
Colaborador Moderador
 
Mensagens: 3126
Registrado em: Seg Dez 14, 2009 11:41
Formação Escolar: GRADUAÇÃO
Andamento: formado
Voltar ao topo
Responder

Voltar para Sistemas de Equações

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes

 


Tópico Popular

Assunto: Taxa de variação
Autor: felipe_ad - Ter Jun 29, 2010 19:44

Como resolvo uma questao desse tipo:

Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?

A letra (a) consegui resolver e cheguei no resultado correto de \frac{4\pi{r}^{2}}{3}
Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é 1,066\pi

Alguem me ajuda? Agradeço desde já.

Assunto: Taxa de variação
Autor: Elcioschin - Qua Jun 30, 2010 20:47

V = (1/3)*pi*r²*h ----> h = 4r/3

V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³

Derivando:

dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3

Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s

Assunto: Taxa de variação
Autor: Guill - Ter Fev 21, 2012 21:17

Temos que o volume é dado por:

V = \frac{4\pi}{3}r^2


Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

\frac{dV}{dt} = \frac{8\pi.r}{3}.\frac{dr}{dt}


Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:

\frac{dV}{dt} = \frac{8\pi.2}{3}.\frac{2}{10}

\frac{dV}{dt} = \frac{16\pi}{15}

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

Índice do fórum