 por exploit » Ter Set 07, 2010 19:17
por exploit » Ter Set 07, 2010 19:17
Olá, estou tendo problema ao realizar a seguinte integração:
![L = \int_{0}^{2\pi} {\sqrt[2]{((1 - cos(t))^2 + {sen(t)}^2)}} dt. L = \int_{0}^{2\pi} {\sqrt[2]{((1 - cos(t))^2 + {sen(t)}^2)}} dt.](/latexrender/pictures/fa4696e70339eed1150fbbf8ac04fc7a.png)
Segundo o gabarito, a resposta é 8. Mas sempre chego na resposta 0. A função primitiva que obtive ao integrar foi
![F(t) = 2\sqrt[2]{2+2cos(t)} F(t) = 2\sqrt[2]{2+2cos(t)}](/latexrender/pictures/f3a9aaccd8a745bed36e166a935be801.png)
Obs.: Realizei duas substituições (u = 1 - cos(t), du = sent(t); e s = 2 - u, ds = du).
Antecipadamente, agradeço a atenção!
[]s,
Exploit
-
exploit
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sex Jul 16, 2010 22:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências de Computação
- Andamento: cursando
 por MarceloFantini » Qua Set 08, 2010 01:30
por MarceloFantini » Qua Set 08, 2010 01:30
Cara, eu tentei resolver mas não obtive resultado (eu chegava até
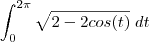
e não conseguia sair). Fui no wolfram, ele resolveu através de várias substituições:
http://www.wolframalpha.com/input/?i=in ... +((1-cos(t))^2+%2B+sen^2(t)+)+dt
Por essa primitiva (sem a cotangente, claro), a resposta dá 8.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por exploit » Qua Set 08, 2010 04:21
por exploit » Qua Set 08, 2010 04:21
Estranho, a resposta não pode ser 8 usando a primitiva
![F(t) = 2 \sqrt[2]{2 cos(t)+2} + constant F(t) = 2 \sqrt[2]{2 cos(t)+2} + constant](/latexrender/pictures/17be99c00195b2fa387fadfb45bcfe2f.png)
. Pois,
![L = \int_{0}^{2\pi} {\sqrt[2]{((1 - cos(t))^2 + {sen(t)}^2)}} dt L = \int_{0}^{2\pi} {\sqrt[2]{((1 - cos(t))^2 + {sen(t)}^2)}} dt](/latexrender/pictures/3663971770db1fb80fcbc8d371775a50.png)
![= 2 \sqrt[2]{2 cos(2\pi)+2} - 2 \sqrt[2]{2 cos(0)+2} = 4 - 4 = 0 = 2 \sqrt[2]{2 cos(2\pi)+2} - 2 \sqrt[2]{2 cos(0)+2} = 4 - 4 = 0](/latexrender/pictures/ebdfda47e176a2f03802593d6b2405b2.png)
. Onde

Além disso, quando tratamos da primitiva "final"
![F(t) = -2 \sqrt[2]{2 - 2cos(t)}cot(t/2) + constant F(t) = -2 \sqrt[2]{2 - 2cos(t)}cot(t/2) + constant](/latexrender/pictures/96e1c4a1cc009857b6b23f24779ef0b7.png)
, sugerida pelo tal WolframAlpha, chegamos a outro impasse, no que tange o seguinte:
![L = \int_{0}^{2\pi} {\sqrt[2]{((1 - cos(t))^2 + {sen(t)}^2)}} dt L = \int_{0}^{2\pi} {\sqrt[2]{((1 - cos(t))^2 + {sen(t)}^2)}} dt](/latexrender/pictures/3663971770db1fb80fcbc8d371775a50.png)
![= -2 \sqrt[2]{2 - 2cos(2\pi)}cot(\pi) - (-2 \sqrt[2]{2 - 2cos(0)}cot(0)) = \infty + \infty = \infty = -2 \sqrt[2]{2 - 2cos(2\pi)}cot(\pi) - (-2 \sqrt[2]{2 - 2cos(0)}cot(0)) = \infty + \infty = \infty](/latexrender/pictures/521a9bcdf2848ab2362ad90a9e255ade.png)
. Onde
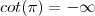
e

Alguém teria outra solução?
-
exploit
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sex Jul 16, 2010 22:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências de Computação
- Andamento: cursando
 por exploit » Qua Set 08, 2010 19:58
por exploit » Qua Set 08, 2010 19:58
Alguém, que entenda bem de Integrais Impróprias, poderia me dizer se devo aplicar o limite na integração? Ou dividir os pontos definidos para duas integrais? Ou ainda alguma outra idéia?
-
exploit
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sex Jul 16, 2010 22:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências de Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] Resolver Integral definida com trigonometria
por rodrigoboreli » Dom Set 07, 2014 01:02
- 1 Respostas
- 4342 Exibições
- Última mensagem por adauto martins

Sex Out 17, 2014 12:39
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo Integral] Integral Definida
por ARCS » Sáb Fev 02, 2013 21:37
- 2 Respostas
- 3677 Exibições
- Última mensagem por e8group

Sáb Fev 02, 2013 22:13
Cálculo: Limites, Derivadas e Integrais
-
- [integral] integral definida por partes
por gabriel feron » Seg Mar 11, 2013 00:48
- 2 Respostas
- 3066 Exibições
- Última mensagem por gabriel feron

Seg Mar 11, 2013 18:19
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Derivar integral definida
por troziinho » Ter Mar 31, 2015 20:26
- 0 Respostas
- 2498 Exibições
- Última mensagem por troziinho

Ter Mar 31, 2015 20:26
Cálculo: Limites, Derivadas e Integrais
-
- integral definida
por liviabgomes » Qua Jun 01, 2011 15:14
- 8 Respostas
- 5942 Exibições
- Última mensagem por carlosalesouza

Qui Jun 02, 2011 12:38
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![L = \int_{0}^{2\pi} {\sqrt[2]{((1 - cos(t))^2 + {sen(t)}^2)}} dt. L = \int_{0}^{2\pi} {\sqrt[2]{((1 - cos(t))^2 + {sen(t)}^2)}} dt.](/latexrender/pictures/fa4696e70339eed1150fbbf8ac04fc7a.png)
![F(t) = 2\sqrt[2]{2+2cos(t)} F(t) = 2\sqrt[2]{2+2cos(t)}](/latexrender/pictures/f3a9aaccd8a745bed36e166a935be801.png)


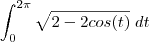 e não conseguia sair). Fui no wolfram, ele resolveu através de várias substituições:
e não conseguia sair). Fui no wolfram, ele resolveu através de várias substituições:

![F(t) = 2 \sqrt[2]{2 cos(t)+2} + constant F(t) = 2 \sqrt[2]{2 cos(t)+2} + constant](/latexrender/pictures/17be99c00195b2fa387fadfb45bcfe2f.png) . Pois,
. Pois,![L = \int_{0}^{2\pi} {\sqrt[2]{((1 - cos(t))^2 + {sen(t)}^2)}} dt L = \int_{0}^{2\pi} {\sqrt[2]{((1 - cos(t))^2 + {sen(t)}^2)}} dt](/latexrender/pictures/3663971770db1fb80fcbc8d371775a50.png)
![= 2 \sqrt[2]{2 cos(2\pi)+2} - 2 \sqrt[2]{2 cos(0)+2} = 4 - 4 = 0 = 2 \sqrt[2]{2 cos(2\pi)+2} - 2 \sqrt[2]{2 cos(0)+2} = 4 - 4 = 0](/latexrender/pictures/ebdfda47e176a2f03802593d6b2405b2.png) . Onde
. Onde 
![F(t) = -2 \sqrt[2]{2 - 2cos(t)}cot(t/2) + constant F(t) = -2 \sqrt[2]{2 - 2cos(t)}cot(t/2) + constant](/latexrender/pictures/96e1c4a1cc009857b6b23f24779ef0b7.png) , sugerida pelo tal WolframAlpha, chegamos a outro impasse, no que tange o seguinte:
, sugerida pelo tal WolframAlpha, chegamos a outro impasse, no que tange o seguinte:![= -2 \sqrt[2]{2 - 2cos(2\pi)}cot(\pi) - (-2 \sqrt[2]{2 - 2cos(0)}cot(0)) = \infty + \infty = \infty = -2 \sqrt[2]{2 - 2cos(2\pi)}cot(\pi) - (-2 \sqrt[2]{2 - 2cos(0)}cot(0)) = \infty + \infty = \infty](/latexrender/pictures/521a9bcdf2848ab2362ad90a9e255ade.png) . Onde
. Onde 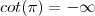 e
e 

 .
.



