De acordo com estudos estatísticos realizados, a quantidade de habitantes de uma determinada região
deve aumentar, nos próximos anos, de acordo com a função P(t)=45.000.
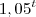 , onde P(t) é a quantidade(aproximada) de habitantes daqui a t anos:
, onde P(t) é a quantidade(aproximada) de habitantes daqui a t anos:a) qual deve ser a quantidade provável (e aproximada) de habitantes desta região daqui a 3 anos?
b)quantos anos(aproximadamente) serão necessários para que a população dessa região dobre de tamanho?









 .
.



