Será que vcx podiam me indicar uma forma de resolução prática e simples que eu pudesse aplicar p/ este tipo de questão? Sou difícil de entender mat.
Sem mais delongas.... aí vai a questão...
O diretor de uma instituição bancária resolveu premiar seus gerentes regionais com a quantia de R$ 36.000,00 em partes iguais. Marcou o dia da distribuição e escreveu no e-mail desse comunicado que, se alguém não comparecesse no dia marcado
o montante seria distribuído entre os presentes, não havendo outra oportunidade. No dia da distribuição, faltaram 3 gerentes e, desse modo, os que compareceram foram beneficiados com R$ 1.000,00 a mais cada um. O total de gerentes regionais dessa instituição bancária é igual a:
a) 5 / b) 6 / c) 7 / d) 8 / e) 12
Obrigada!
Roberta.gmail


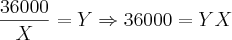
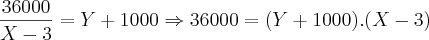
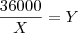 substituimos e deixamos apenas em função de X a equação, que torna-se de 2° grau. Resolvendo, chegamos em um valor positivo e um negativo. Como X é o número de gerentes (ou seja, nao pode ser negativo) consideramos apenas o valor positivo, que é igual a 12.
substituimos e deixamos apenas em função de X a equação, que torna-se de 2° grau. Resolvendo, chegamos em um valor positivo e um negativo. Como X é o número de gerentes (ou seja, nao pode ser negativo) consideramos apenas o valor positivo, que é igual a 12.