1) Se f(x) = x3 + 4x – 3, ache f (1) , f (?1) , f (0) ,
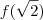
2)Se
 ache f(1), f(3), f(5), f(10)
ache f(1), f(3), f(5), f(10)Grato amigos
Até

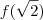
 ache f(1), f(3), f(5), f(10)
ache f(1), f(3), f(5), f(10)
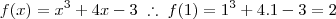

Douglasm escreveu:Bom Duhh, quando se dá uma função f(x) e pede-se f(1), por exemplo, tudo o que se deve fazer é encontrar o valor que a função assume para x = 1. Farei um para que você veja:
Agora é só fazer o mesmo para todas as outras. Até a próxima.

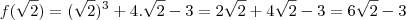


Douglasm escreveu:É a mesma coisa, é só substituirmos:
Na segunda função, novamente, é só substituirmos. Façamos, por exemplo, f(3):
Caso haja mais dúvidas, é só perguntar.


Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.
 :
: