 por jose henrique » Dom Ago 15, 2010 15:08
por jose henrique » Dom Ago 15, 2010 15:08
A expressão :
![\sqrt[]{10+\sqrt[]{10}}X \sqrt[]{10-\sqrt[]{10}}
=\sqrt[]{10}+\sqrt[4]{10}X \sqrt[]{10}- \sqrt[4]{10}
=? \sqrt[]{10+\sqrt[]{10}}X \sqrt[]{10-\sqrt[]{10}}
=\sqrt[]{10}+\sqrt[4]{10}X \sqrt[]{10}- \sqrt[4]{10}
=?](/latexrender/pictures/46a6009bbc99a8be5b9a87e96d426737.png)
partir é que pintou a dúvida da resolução
-
jose henrique
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qui Ago 12, 2010 20:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: outros
- Andamento: formado
 por alexandre32100 » Dom Ago 15, 2010 20:57
por alexandre32100 » Dom Ago 15, 2010 20:57
José,
![\sqrt[]{10+\sqrt[]{10}}\times \sqrt[]{10-\sqrt[]{10}}\not=\sqrt[]{10}+\sqrt[4]{10}\times \sqrt[]{10}- \sqrt[4]{10} \sqrt[]{10+\sqrt[]{10}}\times \sqrt[]{10-\sqrt[]{10}}\not=\sqrt[]{10}+\sqrt[4]{10}\times \sqrt[]{10}- \sqrt[4]{10}](/latexrender/pictures/ec672b806b0de34b7c28553c76309e06.png)
e isto pode ser visto, sei lá, com uma calculadora, se quiser (usei o Google, também dá

)
Mas, o que eu quero dizer é que você não pode dizer que
![\sqrt{10\pm\sqrt{10}}=\sqrt{10}\pm\sqrt[4]{10} \sqrt{10\pm\sqrt{10}}=\sqrt{10}\pm\sqrt[4]{10}](/latexrender/pictures/afb5eb6200a6d950d82a7f5c5c1774cd.png)
. Isto só pode ser feito se você tiver, no lugar da adição (ou subtração), uma multiplicação, pois dai sim pode usar as propriedades das potências (afinal, a raiz não é mais do que uma potência fracionária). Por exemplo:
![\sqrt{10\cdot\sqrt{10}}=(10\cdot10^{\frac{1}{2}})^{\frac{1}{2}}=10^{\frac{1}{2}}\cdot10^{\frac{1}{4}}=\sqrt{10}\cdot\sqrt[4]{10} \sqrt{10\cdot\sqrt{10}}=(10\cdot10^{\frac{1}{2}})^{\frac{1}{2}}=10^{\frac{1}{2}}\cdot10^{\frac{1}{4}}=\sqrt{10}\cdot\sqrt[4]{10}](/latexrender/pictures/4310dc22fd75df4db9b5e965784ce8bf.png)
.
Para resolver este problema, você deve usar uma das propriedades dos "Produtos Notáveis" que diz que
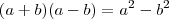
, assim:
![\sqrt[]{10+\sqrt[]{10}}\times \sqrt[]{10-\sqrt[]{10}}=\sqrt{(10+\sqrt{10})(10-\sqrt{10})}} \sqrt[]{10+\sqrt[]{10}}\times \sqrt[]{10-\sqrt[]{10}}=\sqrt{(10+\sqrt{10})(10-\sqrt{10})}}](/latexrender/pictures/464a82ecd7af4a5c22f4fede5fb4ff89.png)
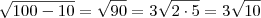
(observe que
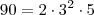
).
-
alexandre32100
-
 por jose henrique » Seg Ago 16, 2010 10:33
por jose henrique » Seg Ago 16, 2010 10:33
obrigado!
-
jose henrique
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qui Ago 12, 2010 20:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: outros
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Raiz Cúbica e Raiz Quadrada] Muito difícil achar a solução.
por Leocondeuba » Sáb Mai 11, 2013 19:27
- 2 Respostas
- 7457 Exibições
- Última mensagem por Leocondeuba

Sáb Mai 11, 2013 20:42
Aritmética
-
- Raiz quadrada
por j1a4l0 » Qui Abr 22, 2010 18:05
- 5 Respostas
- 5990 Exibições
- Última mensagem por Neperiano

Sex Abr 23, 2010 09:35
Funções
-
- raiz quadrada
por jose henrique » Seg Ago 16, 2010 16:54
- 1 Respostas
- 2348 Exibições
- Última mensagem por MarceloFantini

Ter Ago 17, 2010 00:03
Álgebra Elementar
-
- [Raiz quadrada de 13] Na mão
por Mickdark » Dom Abr 08, 2012 20:00
- 4 Respostas
- 17639 Exibições
- Última mensagem por Mickdark

Qui Abr 12, 2012 09:56
Álgebra Elementar
-
- Raiz quadrada
por anneliesero » Qua Dez 12, 2012 19:26
- 1 Respostas
- 2088 Exibições
- Última mensagem por replay

Qua Dez 19, 2012 16:11
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{10+\sqrt[]{10}}X \sqrt[]{10-\sqrt[]{10}}
=\sqrt[]{10}+\sqrt[4]{10}X \sqrt[]{10}- \sqrt[4]{10}
=? \sqrt[]{10+\sqrt[]{10}}X \sqrt[]{10-\sqrt[]{10}}
=\sqrt[]{10}+\sqrt[4]{10}X \sqrt[]{10}- \sqrt[4]{10}
=?](/latexrender/pictures/46a6009bbc99a8be5b9a87e96d426737.png)

![\sqrt[]{10+\sqrt[]{10}}X \sqrt[]{10-\sqrt[]{10}}
=\sqrt[]{10}+\sqrt[4]{10}X \sqrt[]{10}- \sqrt[4]{10}
=? \sqrt[]{10+\sqrt[]{10}}X \sqrt[]{10-\sqrt[]{10}}
=\sqrt[]{10}+\sqrt[4]{10}X \sqrt[]{10}- \sqrt[4]{10}
=?](/latexrender/pictures/46a6009bbc99a8be5b9a87e96d426737.png)

![\sqrt[]{10+\sqrt[]{10}}\times \sqrt[]{10-\sqrt[]{10}}\not=\sqrt[]{10}+\sqrt[4]{10}\times \sqrt[]{10}- \sqrt[4]{10} \sqrt[]{10+\sqrt[]{10}}\times \sqrt[]{10-\sqrt[]{10}}\not=\sqrt[]{10}+\sqrt[4]{10}\times \sqrt[]{10}- \sqrt[4]{10}](/latexrender/pictures/ec672b806b0de34b7c28553c76309e06.png) e isto pode ser visto, sei lá, com uma calculadora, se quiser (usei o Google, também dá
e isto pode ser visto, sei lá, com uma calculadora, se quiser (usei o Google, também dá  )
)![\sqrt{10\pm\sqrt{10}}=\sqrt{10}\pm\sqrt[4]{10} \sqrt{10\pm\sqrt{10}}=\sqrt{10}\pm\sqrt[4]{10}](/latexrender/pictures/afb5eb6200a6d950d82a7f5c5c1774cd.png) . Isto só pode ser feito se você tiver, no lugar da adição (ou subtração), uma multiplicação, pois dai sim pode usar as propriedades das potências (afinal, a raiz não é mais do que uma potência fracionária). Por exemplo:
. Isto só pode ser feito se você tiver, no lugar da adição (ou subtração), uma multiplicação, pois dai sim pode usar as propriedades das potências (afinal, a raiz não é mais do que uma potência fracionária). Por exemplo:![\sqrt{10\cdot\sqrt{10}}=(10\cdot10^{\frac{1}{2}})^{\frac{1}{2}}=10^{\frac{1}{2}}\cdot10^{\frac{1}{4}}=\sqrt{10}\cdot\sqrt[4]{10} \sqrt{10\cdot\sqrt{10}}=(10\cdot10^{\frac{1}{2}})^{\frac{1}{2}}=10^{\frac{1}{2}}\cdot10^{\frac{1}{4}}=\sqrt{10}\cdot\sqrt[4]{10}](/latexrender/pictures/4310dc22fd75df4db9b5e965784ce8bf.png) .
.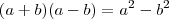 , assim:
, assim:![\sqrt[]{10+\sqrt[]{10}}\times \sqrt[]{10-\sqrt[]{10}}=\sqrt{(10+\sqrt{10})(10-\sqrt{10})}} \sqrt[]{10+\sqrt[]{10}}\times \sqrt[]{10-\sqrt[]{10}}=\sqrt{(10+\sqrt{10})(10-\sqrt{10})}}](/latexrender/pictures/464a82ecd7af4a5c22f4fede5fb4ff89.png)
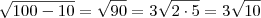 (observe que
(observe que 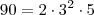 ).
).





