![\sqrt[]{10+\sqrt[]{10}}X \sqrt[]{10-\sqrt[]{10}}
=\sqrt[]{10}+\sqrt[4]{10}X \sqrt[]{10}- \sqrt[4]{10}
=?](/latexrender/pictures/46a6009bbc99a8be5b9a87e96d426737.png "\sqrt[]{10+\sqrt[]{10}}X \sqrt[]{10-\sqrt[]{10}}
=\sqrt[]{10}+\sqrt[4]{10}X \sqrt[]{10}- \sqrt[4]{10}
=?")
partir é que pintou a dúvida da resolução
por jose henrique » Dom Ago 15, 2010 15:08
por alexandre32100 » Dom Ago 15, 2010 20:57
![\sqrt[]{10+\sqrt[]{10}}\times \sqrt[]{10-\sqrt[]{10}}\not=\sqrt[]{10}+\sqrt[4]{10}\times \sqrt[]{10}- \sqrt[4]{10}](/latexrender/pictures/ec672b806b0de34b7c28553c76309e06.png "\sqrt[]{10+\sqrt[]{10}}\times \sqrt[]{10-\sqrt[]{10}}\not=\sqrt[]{10}+\sqrt[4]{10}\times \sqrt[]{10}- \sqrt[4]{10}")
e isto pode ser visto, sei lá, com uma calculadora, se quiser (usei o Google, também dá 
)![\sqrt{10\pm\sqrt{10}}=\sqrt{10}\pm\sqrt[4]{10}](/latexrender/pictures/afb5eb6200a6d950d82a7f5c5c1774cd.png "\sqrt{10\pm\sqrt{10}}=\sqrt{10}\pm\sqrt[4]{10}")
. Isto só pode ser feito se você tiver, no lugar da adição (ou subtração), uma multiplicação, pois dai sim pode usar as propriedades das potências (afinal, a raiz não é mais do que uma potência fracionária). Por exemplo:![\sqrt{10\cdot\sqrt{10}}=(10\cdot10^{\frac{1}{2}})^{\frac{1}{2}}=10^{\frac{1}{2}}\cdot10^{\frac{1}{4}}=\sqrt{10}\cdot\sqrt[4]{10}](/latexrender/pictures/4310dc22fd75df4db9b5e965784ce8bf.png "\sqrt{10\cdot\sqrt{10}}=(10\cdot10^{\frac{1}{2}})^{\frac{1}{2}}=10^{\frac{1}{2}}\cdot10^{\frac{1}{4}}=\sqrt{10}\cdot\sqrt[4]{10}")
.
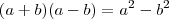, assim:![\sqrt[]{10+\sqrt[]{10}}\times \sqrt[]{10-\sqrt[]{10}}=\sqrt{(10+\sqrt{10})(10-\sqrt{10})}}](/latexrender/pictures/464a82ecd7af4a5c22f4fede5fb4ff89.png "\sqrt[]{10+\sqrt[]{10}}\times \sqrt[]{10-\sqrt[]{10}}=\sqrt{(10+\sqrt{10})(10-\sqrt{10})}}")
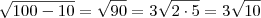(observe que 
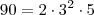).Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
o ângulo entre o eixo horizontal e o afixo 
. O triângulo é retângulo com catetos 
e 
, tal que 
. Seja 
o ângulo complementar. Então 
. Como 
, o ângulo que o afixo 
formará com a horizontal será , mas negativo pois tem de ser no quarto quadrante. Se 
, então 
. Como módulo é um: 
.
.