O que queremos maximizar é a área "S", dada por:
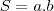
Para podermos verificar o ponto de máximo, devemos primeiro escrever "S" em função de uma variável (nesse caso escolherei "a"). É fácil observar a seguinte relação na circunferência:
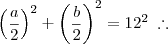
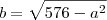
Substituindo em "S":
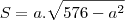
O que temos que fazer agora é encontrar a primeira derivada desta função e igualá-la a zero (posteriormente, a segunda derivada garantirá de que se trata de um ponto de máximo, mas vou omití-la aqui). Logo:
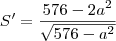
Igualando a zero:
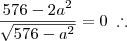
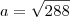
Finalmente, substituindo na relação existente na circunferência, encontramos:
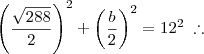
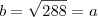
Concluímos que o retângulo com a máxima área a ser inscrito numa circunferência de raio 12 cm é um quadrado de lado

cm.
Obs: Resolvi omitir também o desenvolvimento dos cálculos mas caso haja alguma dúvida nesse sentido é só dizer.
Até a próxima.



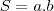
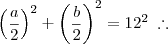
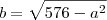
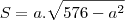
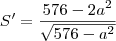
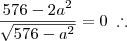
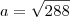
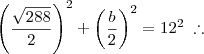
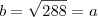
 cm.
cm.
