 que passa por ele durante a hora
que passa por ele durante a hora  , é aproximandamente pela função.
, é aproximandamente pela função.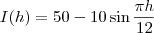
Calcule o horário de pico de tráfego de informação do período de 9h às 21h
alternativas:
a. 18 horas
b. 6 horas
c. 9 horas
d. 6 horas e 18 horas
e. nenhuma das respostas anteriores
poderia explicar como proceder o cálculo, o maior dúvida será é a respeito do sin...
poderia explicar como proceder o cálculo



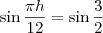
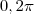 ], o único valor onde o seno tem valor
], o único valor onde o seno tem valor  é
é  . Para que a função seja máxima (ou seja, pico de informação), o seno tem que ser mínimo (-1), por isso que ele igualou o seno.
. Para que a função seja máxima (ou seja, pico de informação), o seno tem que ser mínimo (-1), por isso que ele igualou o seno.

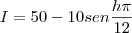 . Quando o seno aumenta, a função diminui, só que nós queremos a função máxima, então o seno tem que ser o MÍNIMO. O seno é mínimo quando vale -1, e o seno só vale -1 quando o arco for
. Quando o seno aumenta, a função diminui, só que nós queremos a função máxima, então o seno tem que ser o MÍNIMO. O seno é mínimo quando vale -1, e o seno só vale -1 quando o arco for 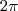 ). Assim, igualamos os senos. Se os senos são iguais, os arcos também iguais devido à restrição feita do intervalo, logo podemos igualar os arcos:
). Assim, igualamos os senos. Se os senos são iguais, os arcos também iguais devido à restrição feita do intervalo, logo podemos igualar os arcos: 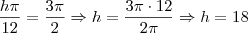 .
.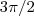
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)