 por gutorocher » Dom Jul 25, 2010 19:40
por gutorocher » Dom Jul 25, 2010 19:40
(POSCOMP-2009) Em um cabo de fibra ótica a quantidade de informação

que passa por ele durante a hora

, é aproximandamente pela função.
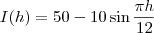
Calcule o horário de pico de tráfego de informação do período de 9h às 21h
alternativas:
a. 18 horas
b. 6 horas
c. 9 horas
d. 6 horas e 18 horas
e. nenhuma das respostas anteriores
poderia explicar como proceder o cálculo, o maior dúvida será é a respeito do sin...
poderia explicar como proceder o cálculo
-

gutorocher
- Usuário Dedicado

-
- Mensagens: 38
- Registrado em: Qua Jul 21, 2010 12:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: CCP
- Andamento: formado
 por gutorocher » Seg Jul 26, 2010 01:45
por gutorocher » Seg Jul 26, 2010 01:45
poderia explica como chegaste
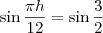
poderia explicar o procedimento que chegaste do lado direito da igualdade pincipalmente o 3 e 2 da onde surgiu.
e o I(h)=50-10 não é feito nenhum cálculo.
-

gutorocher
- Usuário Dedicado

-
- Mensagens: 38
- Registrado em: Qua Jul 21, 2010 12:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: CCP
- Andamento: formado
 por MarceloFantini » Seg Jul 26, 2010 15:45
por MarceloFantini » Seg Jul 26, 2010 15:45
Dentro do intervalo [
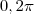
], o único valor onde o seno tem valor

é

. Para que a função seja máxima (ou seja, pico de informação), o seno tem que ser mínimo (-1), por isso que ele igualou o seno.
O resto da função não precisa ser usada pois o problema pede o horário, e não a quantidade de informação.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por gutorocher » Ter Jul 27, 2010 15:26
por gutorocher » Ter Jul 27, 2010 15:26
ainda não conseguir entender o cálculo, poderia mostrar o procedimento
dedde já agradeço as explicações...
-

gutorocher
- Usuário Dedicado

-
- Mensagens: 38
- Registrado em: Qua Jul 21, 2010 12:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: CCP
- Andamento: formado
 por gutorocher » Ter Jul 27, 2010 15:26
por gutorocher » Ter Jul 27, 2010 15:26
..postagem desconsiderada pois ao enviar foi duplicada, considerar a postagem anterior.....
-

gutorocher
- Usuário Dedicado

-
- Mensagens: 38
- Registrado em: Qua Jul 21, 2010 12:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: CCP
- Andamento: formado
 por MarceloFantini » Ter Jul 27, 2010 15:32
por MarceloFantini » Ter Jul 27, 2010 15:32
A função seno varia de -1 a 1. A função é
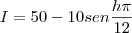
. Quando o seno aumenta, a função diminui, só que nós queremos a função máxima, então o seno tem que ser o MÍNIMO. O seno é mínimo quando vale -1, e o seno só vale -1 quando o arco for

(lembrando que é no intervalo fechado de 0 a
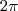
). Assim, igualamos os senos. Se os senos são iguais, os arcos também iguais devido à restrição feita do intervalo, logo podemos igualar os arcos:
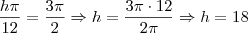
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por MarceloFantini » Sáb Jul 31, 2010 18:38
por MarceloFantini » Sáb Jul 31, 2010 18:38
Eu expliquei. O único arco onde o seno vale -1 (no intervalo [
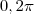
]) é

. Caso tenha dúvidas, sugiro que dê uma revisada em funções circulares (ou trigonométricas).
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por MarceloFantini » Dom Ago 01, 2010 19:03
por MarceloFantini » Dom Ago 01, 2010 19:03
Você já estudou o círculo trigonométrico?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por gutorocher » Dom Ago 01, 2010 19:45
por gutorocher » Dom Ago 01, 2010 19:45
sim já, hoje não me lembro mais e pelo material que eu vi não explica como chegou a esses valores...
vc tem algum material que vc recomendaria para o entendimento melhor...
pois decorar e meio complicado neh... nem sempre cai estas coisas na prova da poscomp
-

gutorocher
- Usuário Dedicado

-
- Mensagens: 38
- Registrado em: Qua Jul 21, 2010 12:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: CCP
- Andamento: formado
 por gutorocher » Qui Ago 05, 2010 16:35
por gutorocher » Qui Ago 05, 2010 16:35
como resolver está questão com uso de derivada
-

gutorocher
- Usuário Dedicado

-
- Mensagens: 38
- Registrado em: Qua Jul 21, 2010 12:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: CCP
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [CALCULO] função composta
por beel » Ter Out 04, 2011 23:44
- 4 Respostas
- 2072 Exibições
- Última mensagem por beel

Qui Out 13, 2011 12:31
Cálculo: Limites, Derivadas e Integrais
-
- Cálculo I - Função do 1 Grau
por jamesramos » Dom Mar 04, 2012 22:49
- 5 Respostas
- 2423 Exibições
- Última mensagem por MarceloFantini

Ter Mar 06, 2012 19:18
Funções
-
- Funcao Trigonometrica Calculo I
por James » Dom Mai 13, 2012 14:05
- 1 Respostas
- 2028 Exibições
- Última mensagem por LuizAquino

Ter Mai 15, 2012 19:40
Cálculo: Limites, Derivadas e Integrais
-
- Calculo de Função vetorial
por cristian9192 » Sex Out 26, 2012 15:18
- 1 Respostas
- 1749 Exibições
- Última mensagem por young_jedi

Sex Out 26, 2012 16:21
Cálculo: Limites, Derivadas e Integrais
-
- Calculo de viga com função.
 por karenblond » Qui Ago 29, 2013 00:06
por karenblond » Qui Ago 29, 2013 00:06
- 4 Respostas
- 11871 Exibições
- Última mensagem por almeidaa_yago

Seg Set 26, 2016 02:28
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 que passa por ele durante a hora
que passa por ele durante a hora  , é aproximandamente pela função.
, é aproximandamente pela função.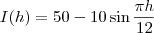



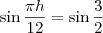
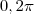 ], o único valor onde o seno tem valor
], o único valor onde o seno tem valor  é
é  . Para que a função seja máxima (ou seja, pico de informação), o seno tem que ser mínimo (-1), por isso que ele igualou o seno.
. Para que a função seja máxima (ou seja, pico de informação), o seno tem que ser mínimo (-1), por isso que ele igualou o seno.

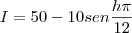 . Quando o seno aumenta, a função diminui, só que nós queremos a função máxima, então o seno tem que ser o MÍNIMO. O seno é mínimo quando vale -1, e o seno só vale -1 quando o arco for
. Quando o seno aumenta, a função diminui, só que nós queremos a função máxima, então o seno tem que ser o MÍNIMO. O seno é mínimo quando vale -1, e o seno só vale -1 quando o arco for 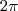 ). Assim, igualamos os senos. Se os senos são iguais, os arcos também iguais devido à restrição feita do intervalo, logo podemos igualar os arcos:
). Assim, igualamos os senos. Se os senos são iguais, os arcos também iguais devido à restrição feita do intervalo, logo podemos igualar os arcos: 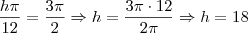 .
.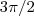


 , avisa que eu resolvo.
, avisa que eu resolvo.

