Tenho de calcular a propagação do erro para uma grandeza que foi calculada baseada em duas outras.
A fórmula é:
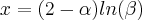
O erro está no
 e no
e no  . Pela formula de propagação de erros sei que tenho de fazer derivadas parciais,. Ou seja, para calcular o erro associado a x tenho de soma a derivada parcial de x em ordem a
. Pela formula de propagação de erros sei que tenho de fazer derivadas parciais,. Ou seja, para calcular o erro associado a x tenho de soma a derivada parcial de x em ordem a  à derivada parcial de x em ordem a
à derivada parcial de x em ordem a  . Podem dar-me uma ajuda? Já não me lembro como isto se faz..
. Podem dar-me uma ajuda? Já não me lembro como isto se faz.. 
Obrigado


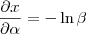
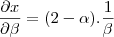

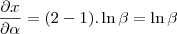
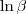 uma constante temos que:
uma constante temos que:![\frac{\partial x}{\partial \alpha} (2- \alpha)*ln \beta = \ln{\beta}*\frac{\partial x}{\partial \alpha} (2- \alpha)=\ln{\beta}*\left[ \frac{\partial x}{\partial \alpha} 2 - \frac{\partial x}{\partial \alpha} \alpha \right]= -\ln{\beta} \frac{\partial x}{\partial \alpha} (2- \alpha)*ln \beta = \ln{\beta}*\frac{\partial x}{\partial \alpha} (2- \alpha)=\ln{\beta}*\left[ \frac{\partial x}{\partial \alpha} 2 - \frac{\partial x}{\partial \alpha} \alpha \right]= -\ln{\beta}](/latexrender/pictures/43294714c7bbd7128a4584e09025c65d.png)

