Exiba o número de funções f com D(f) = {1, 2, 3, 4, 5, 6, 7, 8, 9} e R(f) ? { a, b, c, d, e}, e também com:
a) f(1) ? a e f(9) ? e.
b) f(1) ? f(2), f(1) ? f(3), f(1) ? f(8), f(1) ? f(9) e f(8) ? f(9).
c) R(f) = {a, b, c, d, e}.
d) Número de elementos de f-¹(a) é 3 e o número de elementos de f-¹(b) é menor ou igual a 2.
Sei que é possível resolver pelo Princípio da Inclusão/Exclusão e por Polinômios Cromáticos, mas desconheço a aplicação correta dos dois :s
Se alguém puder me dar uma força ficarei grato!
[]s,
Exploit.
Ps.: TOM, me ajuda!!!!



 e
e 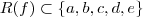 . Pelo Princípio da Inclusão/Exclusão, temos
. Pelo Princípio da Inclusão/Exclusão, temos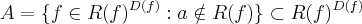
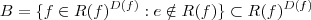
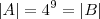 e
e  .
.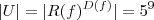 , vem
, vem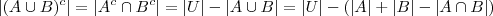

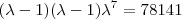 , onde
, onde  .
.

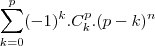
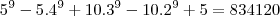

 , ainda restavam as 'cores' 4, 5, 6 e 7 que ficam de fora. Como elas podem aderir a qualquer cor, uma vez que estão desconexas no grafo, o polinômio correto seria
, ainda restavam as 'cores' 4, 5, 6 e 7 que ficam de fora. Como elas podem aderir a qualquer cor, uma vez que estão desconexas no grafo, o polinômio correto seria 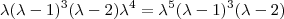 .
.![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.