 por PeIdInHu » Qua Jul 14, 2010 21:04
por PeIdInHu » Qua Jul 14, 2010 21:04
Alguem me ajuda com esse exercicio ......
Encontre p e q tais que g seja contínua e diferenciável em

.Justifique a sua resposta.
(Lembre que uma função f é diferenciável em Dom(f) se existe f'(x) para todo x

Dom(f).)
g(x)= 6x+1 ,se x<3 e
px²+qx ,se x

3
-
PeIdInHu
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Sáb Mai 22, 2010 14:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Imformatica Biomedica
- Andamento: cursando
 por Tom » Qua Jul 14, 2010 23:09
por Tom » Qua Jul 14, 2010 23:09
Como as duas subfunções são polinomiais, então são contínuas e diferenciáveis. Devemos, portanto, apenas fazer que os limites laterais de

quando
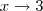
sejam iguais, já que

é, por alto, abscissa do único possível ponto de descontinuidade.
De imediato já temos o limite quando
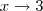
pela esquerda:

; esse deve ser o limite quando
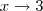
pela direita, isto é:
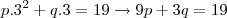
Assim, o conjunto dos pares

que tornam a função diferenciável formam uma reta de equação
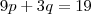
Tom
-
Tom
- Usuário Parceiro

-
- Mensagens: 75
- Registrado em: Sex Jul 02, 2010 00:42
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Automação e Controle Industrial
- Andamento: formado
 por PeIdInHu » Qui Jul 15, 2010 01:03
por PeIdInHu » Qui Jul 15, 2010 01:03
vlwsss =)
-
PeIdInHu
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Sáb Mai 22, 2010 14:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Imformatica Biomedica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Continuidade] Exercício
por fff » Sáb Fev 01, 2014 12:39
- 2 Respostas
- 1548 Exibições
- Última mensagem por fff

Dom Fev 02, 2014 10:23
Cálculo: Limites, Derivadas e Integrais
-
- [Continuidade] Exercício
por fff » Sex Fev 07, 2014 18:10
- 4 Respostas
- 1869 Exibições
- Última mensagem por fff

Sáb Fev 08, 2014 12:41
Cálculo: Limites, Derivadas e Integrais
-
- Continuidade
por AlbertoAM » Seg Abr 04, 2011 20:59
- 8 Respostas
- 5667 Exibições
- Última mensagem por LuizAquino

Qua Abr 06, 2011 10:33
Cálculo: Limites, Derivadas e Integrais
-
- Continuidade
por guilherme5088 » Sáb Out 12, 2019 15:31
- 1 Respostas
- 5326 Exibições
- Última mensagem por adauto martins

Ter Out 15, 2019 23:11
Cálculo: Limites, Derivadas e Integrais
-
- Continuidade
por MCordeiro » Qui Jul 16, 2020 19:11
- 1 Respostas
- 3532 Exibições
- Última mensagem por adauto martins

Qua Out 14, 2020 12:00
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 .Justifique a sua resposta.
.Justifique a sua resposta. Dom(f).)
Dom(f).) 3
3
 .Justifique a sua resposta.
.Justifique a sua resposta. Dom(f).)
Dom(f).) 3
3
 quando
quando 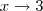 sejam iguais, já que
sejam iguais, já que  é, por alto, abscissa do único possível ponto de descontinuidade.
é, por alto, abscissa do único possível ponto de descontinuidade.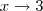 pela esquerda:
pela esquerda: ; esse deve ser o limite quando
; esse deve ser o limite quando 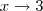 pela direita, isto é:
pela direita, isto é: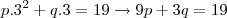
 que tornam a função diferenciável formam uma reta de equação
que tornam a função diferenciável formam uma reta de equação 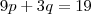


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.