 por Luiza » Ter Jul 13, 2010 12:09
por Luiza » Ter Jul 13, 2010 12:09
Por favor , respondam esssas tres atividades ! OBRIGADA !
1 - se o termo geral d euma P.A é An = 5n-13 , com n \in N* , então a soma de seus 50 primeiros termos é :
2 - Numa PA de três termos tais que sua soma seja 24 e seu produto seja 440 , o primeiro termo pode ser :
3 - O numero de multiplos de 9 entre 105 e 1000 é :
-
Luiza
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Ter Nov 10, 2009 12:28
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Tom » Ter Jul 13, 2010 12:46
por Tom » Ter Jul 13, 2010 12:46
1) Sabemos que numa p.a. o termo geral é dado por:

Conforme o enunciado,

. Fazendo a identidade entre os polinômios, obtemos:

e
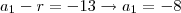
Assim, a soma que queremos obter é :
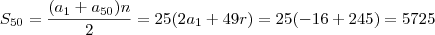
2) Sem perda de generalidade, diremos que os termos da sequência são:
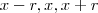
onde

é a razão da progressão. Assim:
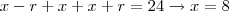

.
Assim, se

então o primeiro termo
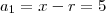
e se
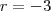
, então o primeiro termo será

3) Os múltiplos de
nove formam uma p.a. de

. Devemos procurar o numero de termos da p.a. compreendidos no intervalo dado.
O primeiro múltiplo de nove, maior que

é

, isto é,

O último múltiplo de nove, menor que

é

, isto é,
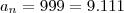
Decorre que:
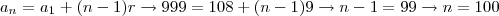
Assim, existem

múltiplos.
Tom
-
Tom
- Usuário Parceiro

-
- Mensagens: 75
- Registrado em: Sex Jul 02, 2010 00:42
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Automação e Controle Industrial
- Andamento: formado
 por Luiza » Ter Jul 13, 2010 13:00
por Luiza » Ter Jul 13, 2010 13:00
Nossa muito obrigada ! agora entendi !
-
Luiza
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Ter Nov 10, 2009 12:28
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 . Fazendo a identidade entre os polinômios, obtemos:
. Fazendo a identidade entre os polinômios, obtemos: e
e 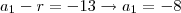
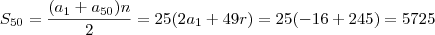
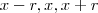 onde
onde  é a razão da progressão. Assim:
é a razão da progressão. Assim: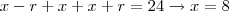
 .
. então o primeiro termo
então o primeiro termo 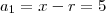 e se
e se 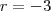 , então o primeiro termo será
, então o primeiro termo será 
 . Devemos procurar o numero de termos da p.a. compreendidos no intervalo dado.
. Devemos procurar o numero de termos da p.a. compreendidos no intervalo dado. é
é  , isto é,
, isto é, 
 é
é  , isto é,
, isto é, 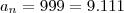
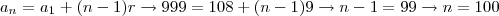
 múltiplos.
múltiplos.