Por favor , respondam esssas tres atividades ! OBRIGADA !
1 - se o termo geral d euma P.A é An = 5n-13 , com n \in N* , então a soma de seus 50 primeiros termos é :
2 - Numa PA de três termos tais que sua soma seja 24 e seu produto seja 440 , o primeiro termo pode ser :
3 - O numero de multiplos de 9 entre 105 e 1000 é :



 . Fazendo a identidade entre os polinômios, obtemos:
. Fazendo a identidade entre os polinômios, obtemos: e
e 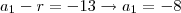
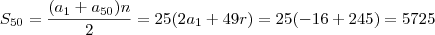
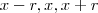 onde
onde  é a razão da progressão. Assim:
é a razão da progressão. Assim: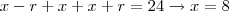
 .
. então o primeiro termo
então o primeiro termo 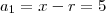 e se
e se 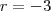 , então o primeiro termo será
, então o primeiro termo será 
 . Devemos procurar o numero de termos da p.a. compreendidos no intervalo dado.
. Devemos procurar o numero de termos da p.a. compreendidos no intervalo dado. é
é  , isto é,
, isto é, 
 é
é  , isto é,
, isto é, 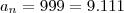
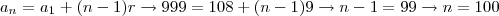
 múltiplos.
múltiplos.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.