![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) do ponto P (3,4).
do ponto P (3,4).Pessoal, tentei fazer o seguinte:
Para uma reta:
y = ax + b
y = 1x + b (pois o a é o coeficiente angular, tg
 = a e no caso do execício,
= a e no caso do execício, 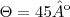 ; tg 45º = 1)
; tg 45º = 1)Como as retas estão com inclinação de 45º em relação ao eixo dos x, trata-se de uma função identidade, em que o coeficiente linear é nulo e o coeficiente angular é 1).
E a outra reta, como faz?
Alguém pode resolver o exercício para mim, passo-a-passo? Estou com dúvidas nessa parte da matéria, estudo sozinho e fica meio complicado. Se alguém puder ajudar, agradeço.


 ,
,  e
e 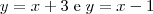

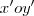 com origem no ponto
com origem no ponto 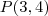 . Para esse sistema, a equação da circunferência em questão é :
. Para esse sistema, a equação da circunferência em questão é : 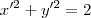 . Ao passo que no sistema de coordenadas convencional a equação seria
. Ao passo que no sistema de coordenadas convencional a equação seria 
 e
e 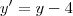
 ; assim obtemos :
; assim obtemos :  e, respeitando a posição dos eixos definidos obtemos os referidos pontos de intercessão
e, respeitando a posição dos eixos definidos obtemos os referidos pontos de intercessão 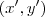 a saber:
a saber: 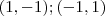
 e
e 
 , isto é,
, isto é, 
 , isto é,
, isto é, 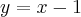
 as retas em questão são:
as retas em questão são: 

 ou
ou 


