 por Fernanda Lauton » Ter Jun 29, 2010 10:35
por Fernanda Lauton » Ter Jun 29, 2010 10:35

já tô ficando nervosa rs

Fernanda lauton
-
Fernanda Lauton
- Usuário Parceiro

-
- Mensagens: 58
- Registrado em: Seg Mar 29, 2010 17:21
- Localização: Minas Gerais
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Biologia
- Andamento: formado
 por DanielFerreira » Ter Jun 29, 2010 19:29
por DanielFerreira » Ter Jun 29, 2010 19:29
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Fernanda Lauton » Qui Jul 01, 2010 08:47
por Fernanda Lauton » Qui Jul 01, 2010 08:47
Muito obrigada aos dois! Agora já não parece mais tão impossível rs
Obrigada mesmo!
Fernanda lauton
-
Fernanda Lauton
- Usuário Parceiro

-
- Mensagens: 58
- Registrado em: Seg Mar 29, 2010 17:21
- Localização: Minas Gerais
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Biologia
- Andamento: formado
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- PARECE FÁCIL - Cálculo de sin(x+y)
por Taah » Dom Mar 28, 2010 13:39
- 6 Respostas
- 4461 Exibições
- Última mensagem por Taah

Seg Mar 29, 2010 16:36
Desafios Difíceis
-
- Limite impossivel !!!!!Respondam urgente!!!!!!!!!!!!!
por luca paula tricolor » Sáb Abr 25, 2015 15:51
- 3 Respostas
- 2771 Exibições
- Última mensagem por DanielFerreira

Dom Abr 26, 2015 13:52
Cálculo: Limites, Derivadas e Integrais
-
- Derivada de uma função trigonométrica [Resposta impossível]
por Matheus Lacombe O » Dom Dez 02, 2012 13:57
- 3 Respostas
- 3110 Exibições
- Última mensagem por DanielFerreira

Dom Dez 02, 2012 17:51
Cálculo: Limites, Derivadas e Integrais
-
- [Sistema Linear Impossivel]Não consigo chegar a resposta.
por Eduardo_rez » Seg Ago 18, 2014 22:59
- 2 Respostas
- 5424 Exibições
- Última mensagem por Eduardo_rez

Ter Ago 19, 2014 15:26
Sistemas de Equações
-
- [INTEGRAL] Integral Impossível... =S
por antonelli2006 » Qua Abr 25, 2012 00:40
- 1 Respostas
- 1972 Exibições
- Última mensagem por Guill

Dom Abr 29, 2012 15:50
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





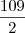
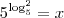





 , avisa que eu resolvo.
, avisa que eu resolvo.

