 por my2009 » Seg Jun 28, 2010 19:14
por my2009 » Seg Jun 28, 2010 19:14
Olá pessoal, tudo bem? estou com um pouco de dificuldade no seguinte exercício: O valor real x para o qual as igualdades sen

= x + 2 e cos

=
![\sqrt[]{} \sqrt[]{}](/latexrender/pictures/fe30ef6b9007d97ba11036078c300fe0.png)
1-x² sejam satisfeitas simultaneamente é:
Resp : -1
Eu tentei resolver esse exercício por meio de uma relação fundamental ( sen²x + cos²x = 1 ) mas não consegui... Por favor, mais uma vez !!! me ajudem ! beijos
-
my2009
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mai 24, 2010 13:57
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Relações
por Rose » Qui Mai 15, 2008 14:41
- 1 Respostas
- 1950 Exibições
- Última mensagem por admin

Qui Mai 15, 2008 16:38
Funções
-
- Relações
por chronoss » Seg Mai 20, 2013 14:19
- 0 Respostas
- 1040 Exibições
- Última mensagem por chronoss

Seg Mai 20, 2013 14:19
Álgebra Elementar
-
- Relações
por livia02 » Qua Set 04, 2013 17:15
- 0 Respostas
- 1115 Exibições
- Última mensagem por livia02

Qua Set 04, 2013 17:15
Álgebra Elementar
-
- [Relações]
por Giudav » Ter Fev 11, 2014 18:38
- 1 Respostas
- 2549 Exibições
- Última mensagem por DanielFerreira

Qua Fev 12, 2014 17:47
Sequências
-
- Relações no círculo
por RBenicio » Qua Set 16, 2009 15:34
- 3 Respostas
- 2819 Exibições
- Última mensagem por Molina

Qui Set 17, 2009 14:45
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 = x + 2 e cos
= x + 2 e cos =
=![\sqrt[]{} \sqrt[]{}](/latexrender/pictures/fe30ef6b9007d97ba11036078c300fe0.png) 1-x² sejam satisfeitas simultaneamente é:
1-x² sejam satisfeitas simultaneamente é: 
 = x + 2 e cos
= x + 2 e cos =
=![\sqrt[]{} \sqrt[]{}](/latexrender/pictures/fe30ef6b9007d97ba11036078c300fe0.png) 1-x² sejam satisfeitas simultaneamente é:
1-x² sejam satisfeitas simultaneamente é: 
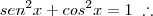
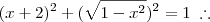
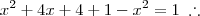
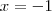

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.