 por gustavowelp » Sáb Jun 26, 2010 11:56
por gustavowelp » Sáb Jun 26, 2010 11:56
Bom dia!
Não entendi o que quer dizer "condição de existência" neste enunciado:
Se a =

, então, satisfazendo as condições de existência, pode-se afirmar que logb a é:
a) – 2
b) – 4
c) -1/2
d) 1/2
e) 2
Muito Obrigado!
-
gustavowelp
- Usuário Parceiro

-
- Mensagens: 91
- Registrado em: Sex Jun 25, 2010 20:40
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: formado
 por Molina » Sáb Jun 26, 2010 16:11
por Molina » Sáb Jun 26, 2010 16:11
gustavowelp escreveu:Bom dia!
Não entendi o que quer dizer "condição de existência" neste enunciado:
Se a =

, então, satisfazendo as condições de existência, pode-se afirmar que logb a é:
a) – 2
b) – 4
c) -1/2
d) 1/2
e) 2
Muito Obrigado!
Boa tarde, Gustavo.
Para existir um logaritmo do tipo
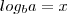
temos que
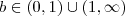
e
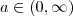
. Ou seja, em outras palavras a base tem que ser maior do que zero e diferente de 1; e o logaritmando tem que ser maior do que zero.
Esta é a condição de existência.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por gustavowelp » Sáb Jun 26, 2010 16:25
por gustavowelp » Sáb Jun 26, 2010 16:25
Obrigado.
Sobre o significado de condição de existência, totalmente explicado; mas qual das alternativas está correta?
Não sei o que deve ser feito para satisfazer tal condição.
Novamente, obrigado Molina!
-
gustavowelp
- Usuário Parceiro

-
- Mensagens: 91
- Registrado em: Sex Jun 25, 2010 20:40
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: formado
 por Molina » Sáb Jun 26, 2010 20:11
por Molina » Sáb Jun 26, 2010 20:11
Boa noite.
Verifique se não há algum erro de digitação nas alternativas da questão, pois meu resultado deu diferente das que tem. Veja:
Considerando
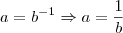
Logo,
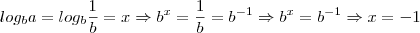
Fico no aguardo de sua confirmação...
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por gustavowelp » Sáb Jun 26, 2010 20:48
por gustavowelp » Sáb Jun 26, 2010 20:48
DESCULPE Molina,
O enunciado que te passei está incorreto!!! Sorry!!!
O correto é: Se a = b^-1 , então, satisfazendo as condições de existência, pode-se afirmar que logb
![\sqrt[]{a} \sqrt[]{a}](/latexrender/pictures/3d48e387f88a173a4e4cf3b38dbab4a6.png)
é...
(Faltou a raiz quadrada...)

A alternativa correta do enunciado é letra C: – 1/2
-
gustavowelp
- Usuário Parceiro

-
- Mensagens: 91
- Registrado em: Sex Jun 25, 2010 20:40
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: formado
 por Molina » Sáb Jun 26, 2010 20:49
por Molina » Sáb Jun 26, 2010 20:49
Sem problemas.
O importante é que você entendeu.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (ITA-72) Condição de Existência
por flavio2010 » Dom Jul 11, 2010 10:03
- 2 Respostas
- 4200 Exibições
- Última mensagem por Tom

Dom Jul 11, 2010 16:00
Álgebra Elementar
-
- Provar a existência de subespaços
por valeuleo » Seg Set 19, 2011 10:52
- 2 Respostas
- 1769 Exibições
- Última mensagem por valeuleo

Seg Set 19, 2011 12:19
Álgebra Linear
-
- Demonstração de existencia de subespaço
por leandro_aur » Dom Mar 04, 2012 19:29
- 0 Respostas
- 1339 Exibições
- Última mensagem por leandro_aur

Dom Mar 04, 2012 19:29
Introdução à Álgebra Linear
-
- [Limite] Conceito de Existência
por eli83 » Qua Out 10, 2012 10:33
- 4 Respostas
- 2574 Exibições
- Última mensagem por young_jedi

Qui Out 11, 2012 17:25
Cálculo: Limites, Derivadas e Integrais
-
- Teorema de Existencia e Unicidade
por Crist » Sex Mar 15, 2013 21:07
- 0 Respostas
- 1313 Exibições
- Última mensagem por Crist

Sex Mar 15, 2013 21:07
Equações Diferenciais Ordinárias e Aplicações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , então, satisfazendo as condições de existência, pode-se afirmar que logb a é:
, então, satisfazendo as condições de existência, pode-se afirmar que logb a é:
 , então, satisfazendo as condições de existência, pode-se afirmar que logb a é:
, então, satisfazendo as condições de existência, pode-se afirmar que logb a é:
, então, satisfazendo as condições de existência, pode-se afirmar que logb a é:
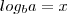 temos que
temos que 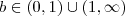 e
e 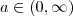 . Ou seja, em outras palavras a base tem que ser maior do que zero e diferente de 1; e o logaritmando tem que ser maior do que zero.
. Ou seja, em outras palavras a base tem que ser maior do que zero e diferente de 1; e o logaritmando tem que ser maior do que zero.


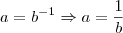
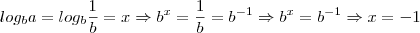

![\sqrt[]{a} \sqrt[]{a}](/latexrender/pictures/3d48e387f88a173a4e4cf3b38dbab4a6.png) é...
é...



 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.