Boa noite, Fernanda.
Talvez seja mais fácil explicar essa propriedade pessoalmente do que pelo livro, fórum, etc. Mas vamos tentar:
Você pode começar pensando que exponencial e logaritmo são operações opostas, assim como adição e subtração por exemplo, ou multiplicação e divisão.
No caso da adição e subtração, se você tem um número B e soma e subtrai A, você obtém como resposta o B:

No caso da multiplicação e divisão, se você tem um número B e multiplica e divide por A, você obtém como resposta o B:

Isso é fácil de perceber, não é?
Agora você pode usar as mesmas informações para exponencial e logaritmo. Se você tem um número B e faz o logaritmo desse número na base A e faz A elevado a esse número, você obtém o B inicial:

Este é o primeiro passo para você começar a compreender o assunto. Agora vou tentar explicar de outra maneira o que o livro quis dizer:
Digamos que queremos descobrir quanto vale

. Suponhamos que não sabemos desta propriedade e veremos se chegaremos nela sem utilizá-la:
 (equação 1)
(equação 1)considerando

, pela propriedade de logaritmos temos que
 (equação 2)
(equação 2)Vou reescrever a equação 1 só que ao invés de usar b, vou usar
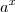
, já que são iguais pela equação 2:

Tem uma propriedade no logaritmo que diz que quando tiver um expoente no logaritmando, eu posso passa-lo pra frente do log na forma de multiplicação:

Outra propriedade do logaritmo diz que quando o logaritmando e a base forem iguais, esse log é igual a 1, pois
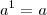
:

Mas pela equação 2, temos que:

Ou seja, voltando todos os passos temos que
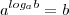
Que era onde queríamos chegar, sem usar esta propriedade.
Leia, releia e releia novamente que você vai compreender.
Qualquer dúvida, informe!

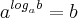
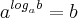 , pois fazendo
, pois fazendo 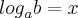 , temos
, temos 
 Mas e o 'a' a que todo esse logaritmo estava elevado
Mas e o 'a' a que todo esse logaritmo estava elevado 

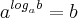
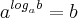 , pois fazendo
, pois fazendo 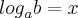 , temos
, temos 
 Mas e o 'a' a que todo esse logaritmo estava elevado
Mas e o 'a' a que todo esse logaritmo estava elevado 




 . Suponhamos que não sabemos desta propriedade e veremos se chegaremos nela sem utilizá-la:
. Suponhamos que não sabemos desta propriedade e veremos se chegaremos nela sem utilizá-la: (equação 1)
(equação 1) , pela propriedade de logaritmos temos que
, pela propriedade de logaritmos temos que  (equação 2)
(equação 2)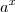 , já que são iguais pela equação 2:
, já que são iguais pela equação 2:

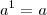 :
:

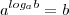




 .
.
 :
: