 por Carolziiinhaaah » Qua Jun 16, 2010 18:31
por Carolziiinhaaah » Qua Jun 16, 2010 18:31
Determine o conjunto de todos os valores reais

tal que

, para os quais a1, a2, a3 formam, nessa ordem, uma PG de razão

e representam as medidas dos lados de um triângulo.
gabarito:
![q \in1 \;\;] 1 \frac{\sqrt[]{5}+1}{2}[ q \in1 \;\;] 1 \frac{\sqrt[]{5}+1}{2}[](/latexrender/pictures/636ee168a27bde75c4f872fdd5246084.png)
-

Carolziiinhaaah
- Usuário Parceiro

-
- Mensagens: 77
- Registrado em: Sex Mai 28, 2010 14:12
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Douglasm » Qua Jun 16, 2010 20:56
por Douglasm » Qua Jun 16, 2010 20:56
Boa noite. Para resolver essa questão vamos fazer uso de uma desigualdade presente em qualquer triângulo: o lado maior sempre será menor que a soma dos outros dois.
Vamos chamar os lados de
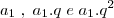
(em ordem crescente, notando que os lados formam uma P.G.).
Agora é só aplicar a desigualdade:
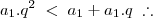
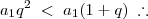

Essa inequação nos dá como resultado o intervalo
![\left]\frac{1-\sqrt{5}}{2} \; , \; \frac{1+\sqrt{5}}{2}\right[ \left]\frac{1-\sqrt{5}}{2} \; , \; \frac{1+\sqrt{5}}{2}\right[](/latexrender/pictures/a05a67dc7a982df24d0ff576dc47dd40.png)
.
Mas como sabemos que q > 1, ficamos com:
![q \; \in \; \left]1 \; , \; \frac{1+\sqrt{5}}{2}\right[ q \; \in \; \left]1 \; , \; \frac{1+\sqrt{5}}{2}\right[](/latexrender/pictures/a9d5b3d50488f849344068fca9076895.png)
E está ai a resposta. Até a próxima.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Carolziiinhaaah » Qua Jun 16, 2010 21:00
por Carolziiinhaaah » Qua Jun 16, 2010 21:00
Show

Valeu Douglas!
-

Carolziiinhaaah
- Usuário Parceiro

-
- Mensagens: 77
- Registrado em: Sex Mai 28, 2010 14:12
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Questão POSCOMP 2011] Ajuda para interpretar questão
por hlustosa » Dom Jul 29, 2012 14:54
- 3 Respostas
- 12987 Exibições
- Última mensagem por hlustosa

Seg Jul 30, 2012 01:13
Funções
-
- Questão de P.A.
por mushthielv » Seg Ago 17, 2009 12:21
- 2 Respostas
- 10968 Exibições
- Última mensagem por Elcioschin

Ter Ago 18, 2009 08:54
Progressões
-
- QUESTÃO
por GABRIELA » Ter Set 08, 2009 16:32
- 2 Respostas
- 15111 Exibições
- Última mensagem por GABRIELA

Ter Set 08, 2009 21:21
Matrizes e Determinantes
-
- Questão da FCC
por wanderlymarques » Qua Nov 18, 2009 12:44
- 2 Respostas
- 5026 Exibições
- Última mensagem por wanderlymarques

Qui Nov 19, 2009 12:58
Cálculo: Limites, Derivadas e Integrais
-
- questão
por sirle ignes » Seg Mar 08, 2010 23:46
- 2 Respostas
- 4792 Exibições
- Última mensagem por sirle ignes

Ter Mar 09, 2010 17:32
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 tal que
tal que  , para os quais a1, a2, a3 formam, nessa ordem, uma PG de razão
, para os quais a1, a2, a3 formam, nessa ordem, uma PG de razão e representam as medidas dos lados de um triângulo.
e representam as medidas dos lados de um triângulo.![q \in1 \;\;] 1 \frac{\sqrt[]{5}+1}{2}[ q \in1 \;\;] 1 \frac{\sqrt[]{5}+1}{2}[](/latexrender/pictures/636ee168a27bde75c4f872fdd5246084.png)

 tal que
tal que  , para os quais a1, a2, a3 formam, nessa ordem, uma PG de razão
, para os quais a1, a2, a3 formam, nessa ordem, uma PG de razão e representam as medidas dos lados de um triângulo.
e representam as medidas dos lados de um triângulo.![q \in1 \;\;] 1 \frac{\sqrt[]{5}+1}{2}[ q \in1 \;\;] 1 \frac{\sqrt[]{5}+1}{2}[](/latexrender/pictures/636ee168a27bde75c4f872fdd5246084.png)

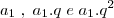 (em ordem crescente, notando que os lados formam uma P.G.).
(em ordem crescente, notando que os lados formam uma P.G.).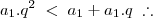
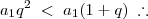

![\left]\frac{1-\sqrt{5}}{2} \; , \; \frac{1+\sqrt{5}}{2}\right[ \left]\frac{1-\sqrt{5}}{2} \; , \; \frac{1+\sqrt{5}}{2}\right[](/latexrender/pictures/a05a67dc7a982df24d0ff576dc47dd40.png) .
. ![q \; \in \; \left]1 \; , \; \frac{1+\sqrt{5}}{2}\right[ q \; \in \; \left]1 \; , \; \frac{1+\sqrt{5}}{2}\right[](/latexrender/pictures/a9d5b3d50488f849344068fca9076895.png)

 Valeu Douglas!
Valeu Douglas!
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.