 por elis81 » Qui Abr 15, 2010 20:20
por elis81 » Qui Abr 15, 2010 20:20
Alguém poderia me ajudar a fazer o seguinte exercício?
a)Mostre que v=(a,b) e w(-b,a) são vetores ortogonais;
b) Use o resultado da parte (a) para encontrar dois vetores ortogonais a v=(2,-3);
c) encontre dois vetores unitários que são ortogonais a (-3,4)
-
elis81
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qui Abr 15, 2010 20:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por Mathmatematica » Dom Jun 13, 2010 01:25
por Mathmatematica » Dom Jun 13, 2010 01:25
a) Dois vetores são ortogonais, ou seja, perpendiculares se, e somente se, o produto escalar dos dois der zero. Logo:

-
Mathmatematica
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Sex Jun 04, 2010 23:53
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado
- Andamento: cursando
 por Mathmatematica » Dom Jun 13, 2010 01:30
por Mathmatematica » Dom Jun 13, 2010 01:30
b) Seguindo a técnica do item a, para obtermos um vetor perpendicular a outro basta conservar uma de suas coordenadas e usar o inverso aditivo na outra. Em seguida, troque a abscissa pela ordenada. Logo, os dois vetores procurados são

.
-
Mathmatematica
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Sex Jun 04, 2010 23:53
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado
- Andamento: cursando
 por Mathmatematica » Dom Jun 13, 2010 01:41
por Mathmatematica » Dom Jun 13, 2010 01:41
c) Seja

um vetor procurado.
Sabemos que esse vetor é unitário. Então,

.
Sabemos também que esse vetor é perpendicutar ao vetor

. Logo,

.
Fazendo
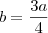
e substituindo em
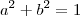
temos:
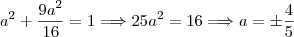
Para
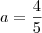
temos

.
Para
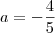
temos

.
Logo, os vetores procurados são
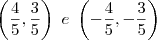
.
Bons estudos Elis.
Observações:
_Qualquer erro, por favor, AVISEM!!!!!!!!!!!
-
Mathmatematica
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Sex Jun 04, 2010 23:53
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida em vetor
por elis81 » Qui Abr 15, 2010 20:22
- 2 Respostas
- 4663 Exibições
- Última mensagem por elis81

Qui Abr 29, 2010 17:01
Geometria Analítica
-
- Duvida vetor gradiente
por VenomForm » Qui Nov 14, 2013 11:21
- 2 Respostas
- 5347 Exibições
- Última mensagem por adauto martins

Qui Set 24, 2015 15:38
Cálculo: Limites, Derivadas e Integrais
-
- Duvida na aplicação de Modulo no vetor
por PatyMCastro » Qua Abr 20, 2011 14:47
- 6 Respostas
- 3541 Exibições
- Última mensagem por PatyMCastro

Qua Abr 27, 2011 00:34
Geometria Analítica
-
- (Vetor Colinear) Dúvida Conceitual
por Man Utd » Sáb Abr 20, 2013 17:42
- 5 Respostas
- 7056 Exibições
- Última mensagem por LuizAquino

Seg Abr 29, 2013 17:05
Geometria Analítica
-
- [CURVAS] ângulo entre vetor tangente e vetor posição
por inkz » Ter Nov 20, 2012 01:24
- 5 Respostas
- 4917 Exibições
- Última mensagem por LuannLuna

Qui Nov 29, 2012 15:05
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




 .
. um vetor procurado.
um vetor procurado.  .
. . Logo,
. Logo,  .
.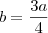 e substituindo em
e substituindo em 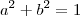 temos:
temos: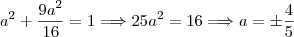
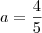 temos
temos  .
. temos
temos  .
.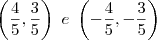 .
.
 .
.
 :
: