 por elis81 » Qui Abr 15, 2010 20:20
por elis81 » Qui Abr 15, 2010 20:20
Alguém poderia me ajudar a fazer o seguinte exercício?
a)Mostre que v=(a,b) e w(-b,a) são vetores ortogonais;
b) Use o resultado da parte (a) para encontrar dois vetores ortogonais a v=(2,-3);
c) encontre dois vetores unitários que são ortogonais a (-3,4)
-
elis81
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qui Abr 15, 2010 20:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por Mathmatematica » Dom Jun 13, 2010 01:25
por Mathmatematica » Dom Jun 13, 2010 01:25
a) Dois vetores são ortogonais, ou seja, perpendiculares se, e somente se, o produto escalar dos dois der zero. Logo:

-
Mathmatematica
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Sex Jun 04, 2010 23:53
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado
- Andamento: cursando
 por Mathmatematica » Dom Jun 13, 2010 01:30
por Mathmatematica » Dom Jun 13, 2010 01:30
b) Seguindo a técnica do item a, para obtermos um vetor perpendicular a outro basta conservar uma de suas coordenadas e usar o inverso aditivo na outra. Em seguida, troque a abscissa pela ordenada. Logo, os dois vetores procurados são

.
-
Mathmatematica
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Sex Jun 04, 2010 23:53
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado
- Andamento: cursando
 por Mathmatematica » Dom Jun 13, 2010 01:41
por Mathmatematica » Dom Jun 13, 2010 01:41
c) Seja

um vetor procurado.
Sabemos que esse vetor é unitário. Então,

.
Sabemos também que esse vetor é perpendicutar ao vetor

. Logo,

.
Fazendo
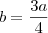
e substituindo em
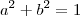
temos:
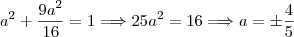
Para
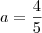
temos

.
Para
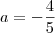
temos

.
Logo, os vetores procurados são
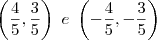
.
Bons estudos Elis.
Observações:
_Qualquer erro, por favor, AVISEM!!!!!!!!!!!
-
Mathmatematica
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Sex Jun 04, 2010 23:53
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida em vetor
por elis81 » Qui Abr 15, 2010 20:22
- 2 Respostas
- 4652 Exibições
- Última mensagem por elis81

Qui Abr 29, 2010 17:01
Geometria Analítica
-
- Duvida vetor gradiente
por VenomForm » Qui Nov 14, 2013 11:21
- 2 Respostas
- 5334 Exibições
- Última mensagem por adauto martins

Qui Set 24, 2015 15:38
Cálculo: Limites, Derivadas e Integrais
-
- Duvida na aplicação de Modulo no vetor
por PatyMCastro » Qua Abr 20, 2011 14:47
- 6 Respostas
- 3527 Exibições
- Última mensagem por PatyMCastro

Qua Abr 27, 2011 00:34
Geometria Analítica
-
- (Vetor Colinear) Dúvida Conceitual
por Man Utd » Sáb Abr 20, 2013 17:42
- 5 Respostas
- 7046 Exibições
- Última mensagem por LuizAquino

Seg Abr 29, 2013 17:05
Geometria Analítica
-
- [CURVAS] ângulo entre vetor tangente e vetor posição
por inkz » Ter Nov 20, 2012 01:24
- 5 Respostas
- 4897 Exibições
- Última mensagem por LuannLuna

Qui Nov 29, 2012 15:05
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




 .
. um vetor procurado.
um vetor procurado.  .
. . Logo,
. Logo,  .
.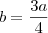 e substituindo em
e substituindo em 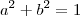 temos:
temos: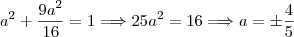
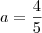 temos
temos  .
. temos
temos  .
.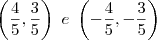 .
. .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
