 por hevhoram » Qui Jun 03, 2010 20:29
por hevhoram » Qui Jun 03, 2010 20:29
Uma jarra contém uma mistura de suco de laranja com água, na proporção de 1 para 3, e outra jarra contém uma mistura de suco de laranja com água na proporção de 1 para 5. Misturando partes iguais dos conteúdos das jarras, obteremos uma mistura de suco de laranja com água na proporção de :
Resposta: 5 para 19
1/3 + 1/5 = 8/15 não entendi o que é pra fazer alguém pode me dar uma luz?
-

hevhoram
- Usuário Parceiro

-
- Mensagens: 61
- Registrado em: Qua Jun 02, 2010 11:43
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: informática educacional
- Andamento: formado
 por Neperiano » Dom Jun 06, 2010 14:33
por Neperiano » Dom Jun 06, 2010 14:33
Ola
Tenho que ressaltar que esta questão apesar de parecer fácil é bem complicadinha
Bom primeiro voce tenque se dar conta que não basta somar uma com a outra, pois voce precisa pegar partes iguais
Então primeiro voce precisa determinar quanto de laranja e água tem numa mistura, pegue 1 litro de cada mistura
Na mistura A
Em 1 litro de mistura vai ter:
0,75 ml de Água
0,25 ml de Laranja
Na mistura B
Em 1 litro:
0,83 de Água
0,16 de Laranja
Agora voce deve somar
Laranja da A + B e Água da A + B
Que vai dar
0,41/1,58=0,25
5/19 =0,26
É praticamente a mesma coisa mudou pelo arredondamento das casas
Note que voce poderia resolver por fração tambem, para tanto na hora de igualar as quantidades em 1 litro, voce deveria utilizar fração, exemplo:
Mistura A,
3/4 de Água, 1/4 de Laranja
Fazer o mesmo com a mistura B e somar
Espero ter ajudado
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por MarceloFantini » Seg Jun 07, 2010 19:04
por MarceloFantini » Seg Jun 07, 2010 19:04
Não é tão dificil Maligno, veja: o suco A tem 4 partes, sendo que a água é
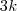
e o suco
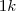
, tendo então
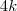
. O suco B, analogamente, tem
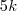
e

, totalizando
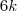
. Queremos um suco C tal que a razão entre suco A e suco B seja um, ou seja, mesma proporção (ou proporção iguais). Para que tenham proporções iguais, o suco A tem que ser usado três vezes e o suco B duas vezes. Logo, a proporção dos componentes será a soma:
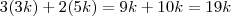
de água e
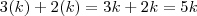
de suco.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Neperiano » Ter Jun 08, 2010 15:12
por Neperiano » Ter Jun 08, 2010 15:12
Ola
É tambem da para resolver assim não quis dizer no sentido de dificil mas no sentido de pega ratão, muita gente cai nessa, soma direto.
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [proporcionalidade] Indústrias de suco concentrado
por admin » Qua Dez 12, 2007 03:10
- 1 Respostas
- 2084 Exibições
- Última mensagem por admin

Qua Dez 12, 2007 03:19
Álgebra Elementar
-
- razão questão da tinta azul claro
por hevhoram » Qui Jun 03, 2010 20:32
- 1 Respostas
- 8802 Exibições
- Última mensagem por MarceloFantini

Sex Jun 04, 2010 16:32
Álgebra Elementar
-
- RAZÃO
por hevhoram » Qua Jun 02, 2010 11:50
- 1 Respostas
- 1535 Exibições
- Última mensagem por Molina

Qua Jun 02, 2010 18:43
Álgebra Elementar
-
- razao
por hevhoram » Qua Jun 02, 2010 20:14
- 2 Respostas
- 1681 Exibições
- Última mensagem por hevhoram

Qui Jun 03, 2010 20:42
Álgebra Elementar
-
- Razão
por Guaciara » Qui Set 23, 2010 22:40
- 2 Respostas
- 2408 Exibições
- Última mensagem por Guaciara

Qui Set 23, 2010 23:31
Conversão de Unidades
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



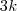 e o suco
e o suco 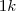 , tendo então
, tendo então 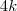 . O suco B, analogamente, tem
. O suco B, analogamente, tem 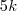 e
e  , totalizando
, totalizando 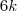 . Queremos um suco C tal que a razão entre suco A e suco B seja um, ou seja, mesma proporção (ou proporção iguais). Para que tenham proporções iguais, o suco A tem que ser usado três vezes e o suco B duas vezes. Logo, a proporção dos componentes será a soma:
. Queremos um suco C tal que a razão entre suco A e suco B seja um, ou seja, mesma proporção (ou proporção iguais). Para que tenham proporções iguais, o suco A tem que ser usado três vezes e o suco B duas vezes. Logo, a proporção dos componentes será a soma: 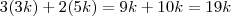 de água e
de água e 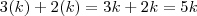 de suco.
de suco.
