 por jones_slash » Dom Jun 06, 2010 10:42
por jones_slash » Dom Jun 06, 2010 10:42
Ai galera alguem sabe mostrar q quando calculamos 3 elevado a n
o algarismo das unidades representado na base 10 só pode ser
1,3,7,9 para todo n E N ?????
-
jones_slash
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sáb Jun 05, 2010 17:05
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico em eletrotecnica e eletronica
- Andamento: formado
 por davi_11 » Seg Jun 07, 2010 16:35
por davi_11 » Seg Jun 07, 2010 16:35
É mesma coisa que dizer que 10 divide

Ou que 2 e 5 dividem

simultaneamente.
É claro que 2 divide, pois qualquer potência de n° ímpar é necessariamente um número ímpar.
Dizer que 5 divide

é mesma coisa que dizer que
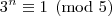
, ou

, ou

, ou

Basta provar apenas que 5 não divide
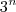
, o que é claro, já que
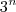
só possui 3 como fatores primos.
Espero não ter sido confuso ou cometido algum equivoco.
"Se é proibido pisar na grama, o jeito é deitar e rolar..."
-
davi_11
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Sex Abr 02, 2010 22:47
- Localização: Leme - SP
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Curso técnico em eletrotécnica
- Andamento: formado
 por jones_slash » Seg Jun 07, 2010 22:44
por jones_slash » Seg Jun 07, 2010 22:44
Pow cara valeu mesmo !!!!!!!!!
Tenho uma prova quinta-feira e
essa era uma das questões q eu
nem sabia por onde começar !!!!
Valeuu
-
jones_slash
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sáb Jun 05, 2010 17:05
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico em eletrotecnica e eletronica
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Aritmética] Algarismo das unidades
por Russman » Qui Jan 17, 2013 01:28
- 4 Respostas
- 7308 Exibições
- Última mensagem por DanielFerreira

Qui Jan 17, 2013 06:58
Aritmética
-
- Algarismo que ocupa a ordem das unidades
por Cleyson007 » Dom Jan 10, 2010 18:28
- 1 Respostas
- 9427 Exibições
- Última mensagem por MarceloFantini

Dom Jan 10, 2010 20:43
Estatística
-
- UFI- Algarismo da unidade
por Maria Livia » Ter Mar 12, 2013 21:52
- 1 Respostas
- 1581 Exibições
- Última mensagem por DanielFerreira

Ter Mar 12, 2013 22:56
Álgebra Elementar
-
- Limite + algarismo de Euler = ????
por EulaCarrara » Seg Abr 19, 2010 21:29
- 5 Respostas
- 4022 Exibições
- Última mensagem por MarceloFantini

Seg Abr 19, 2010 23:11
Cálculo: Limites, Derivadas e Integrais
-
- Sucessão e quantidade de vezes de repetição de algarismo
por remoreiraaa » Qua Jan 06, 2010 20:26
- 1 Respostas
- 3589 Exibições
- Última mensagem por Molina

Sex Jan 08, 2010 13:53
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




 simultaneamente.
simultaneamente. é mesma coisa que dizer que
é mesma coisa que dizer que 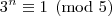 , ou
, ou  , ou
, ou  , ou
, ou 
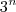 , o que é claro, já que
, o que é claro, já que 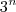 só possui 3 como fatores primos.
só possui 3 como fatores primos.
