Estou com algumas duvidas em relação ao uso de limites e entre elas a que não consigo visualizar o andamento após aplicar regras de derivador por exemplo:
Tenho a seguinte função a derivar:

A regra da soma diz de forma simples ( A derivada do termo a + a derivada do termo b ..... n );
Utilizando a regras da raiz:
 , então utiliza-se a derivada de u'/k.
, então utiliza-se a derivada de u'/k.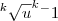
Obs: não consegui expressar utilizando o LaTeX ( Ler-se derivada de u sobre k vezes raiz de u, elevado a k menos 1, sendo k o valor da raiz. ):
Obtendo a resposta utilizando esta regra, devo parar neste ponto ou devo continuar, utilizando mmc etc? Como faço?
A minha segunda duvida esta reclacionado quando a partir do resultado de uma derivida encontramos outra derivida, podemos continuar derivando até que momento? Ou devo aplicar a regra das derivadas apenas para obter o primeiro resultado e o resto é so calcular, produtos notaveis, etc?
Se alguem tiver algum material que possa tirar essas minhas duvidas agradeço.
Obrigado a todos pela atenção;





![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)