 por thais silva » Qua Mai 19, 2010 17:30
por thais silva » Qua Mai 19, 2010 17:30
Afim de atrair clientes, uma companhia de ônibus que liga São Paulo a Campinas laçou a seguinte promoçao:
1-preço de um trecho (ida ou volta) R$ 11,00
2- após a 15° viagem em um mes, cada trecho comprado nesse mesmo mes sai por R$ 9,00
a) Tres passageiros A, B e C embarcaram, respectivamente, em 8, 16 e 20 trechos. Quanto gastou cada um?
b) Determine o gasto g de um individuo que utilizou o serviço durante x(x > 15) dias no mes
c) Quantos trechos podem ser percorridas em um mes, dispondo-se de R$ 200,00?
Eu tentei fazer:
1 = 11a + b
165 = 9a + b
Só que nao deu certo (o 165 veio da multiplicaçao 11*15)
-
thais silva
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Abr 09, 2010 16:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Qui Mai 20, 2010 02:30
por MarceloFantini » Qui Mai 20, 2010 02:30
Passageiro A:

reais.
Passageiro B:
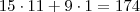
reais.
Passageiro C:

reais.
Gasto: seja g(x) a função que representa o gasto, onde

.
Com 200 reais, podem-se realizer 18 trechos em um mesmo mês.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por marcellef » Seg Jul 12, 2010 21:46
por marcellef » Seg Jul 12, 2010 21:46
Mas não tem como fazer uma equação só para as duas situações?
-
marcellef
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Jul 12, 2010 21:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: DIREITO
- Andamento: formado
 por MarceloFantini » Seg Jul 12, 2010 22:04
por MarceloFantini » Seg Jul 12, 2010 22:04
Não, pois tem comportamentos diferentes.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Função afim] Determinar a função afim
por Apprentice » Dom Set 30, 2012 21:49
- 4 Respostas
- 3237 Exibições
- Última mensagem por Apprentice

Seg Out 01, 2012 12:19
Funções
-
- funçao afim
por maiara amaral » Dom Mai 11, 2008 18:08
- 2 Respostas
- 4875 Exibições
- Última mensagem por Kabarosk

Sex Mai 29, 2015 01:45
Pedidos
-
- funçao afim
por emilly » Ter Ago 17, 2010 20:40
- 6 Respostas
- 7224 Exibições
- Última mensagem por emilly

Qui Ago 19, 2010 18:32
Funções
-
- Função Afim
por Kelvin Brayan » Ter Mai 31, 2011 01:59
- 1 Respostas
- 2932 Exibições
- Última mensagem por Kelvin Brayan

Ter Jun 07, 2011 16:29
Funções
-
- Função Afim
por lihsecundo » Qui Set 01, 2011 19:25
- 1 Respostas
- 1612 Exibições
- Última mensagem por MarceloFantini

Qui Set 01, 2011 19:57
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 reais.
reais.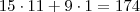 reais.
reais. reais.
reais. .
.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.