 por Skcedas » Ter Mai 18, 2010 21:17
por Skcedas » Ter Mai 18, 2010 21:17
To fazendo uma pa de questões aqui ,essas duas não sei por qual motivo não esta batendo minha respostas com gabarito, e tenho quase certeza que o gabarito esta certo
1)
Seja R(x) a razao entre P(x) = 2x² + 4x - 30 e Q(x) = -3x² - 3x + 36 para quais valores de x, R(x) é negativa?
2)
Sendo f uma funçao par e g uma funçao impar e sabendo-se que f(-?) = ?2 e g(-?2)=?, pode se concluir que (fog)(?2) é igual a:
gabarito
1)(-?,-5) U (-4,?)
2)?2
-
Skcedas
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Ter Mai 18, 2010 20:52
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Douglasm » Ter Mai 18, 2010 22:22
por Douglasm » Ter Mai 18, 2010 22:22
Olá Skcedas.
1) Primeiro vemos que:
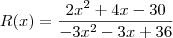
É fácil verificar as raízes de ambas as equações e fatorá-las:
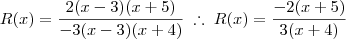
Agora devemos analisar as condições para que R(x) seja negativa, mais precisamente, isso indica que devemos analisar as situações em que o denominador e o numerador apresentem sinais diferentes:
1º.
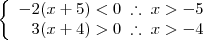
Assim a primeira condição é
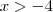
.
2º.
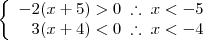
A segunda condição fica sendo
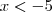
.
Finalmente, os intervalos considerados são:
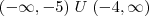
2) Aqui se trata apenas de uma função composta:
![fog(x) = f[g(x)] fog(x) = f[g(x)]](/latexrender/pictures/5fc1a848713041c51f0b0b0bf901805f.png)
Deste modo:
![fog(\sqrt{2}) = f[g(\sqrt{2})] fog(\sqrt{2}) = f[g(\sqrt{2})]](/latexrender/pictures/33221b6d2ac008f45bb1b3cf5aff0ab7.png)
Preste atenção agora: como g é uma função ímpar, isso implica que
g(-x) = -g(x). Logo:
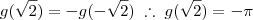
Agora é só finalizarmos:
![fog(\sqrt{2}) = f[g(\sqrt{2})] = f(-\pi) = \sqrt{2} fog(\sqrt{2}) = f[g(\sqrt{2})] = f(-\pi) = \sqrt{2}](/latexrender/pictures/cd491170c94854e4e3e35879d512a096.png)
Até a próxima.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [gráfico de função] Dúvida em questões do CESPE
por rogerioandre » Qua Jun 06, 2012 19:07
- 1 Respostas
- 1350 Exibições
- Última mensagem por Russman

Qua Jun 06, 2012 23:26
Funções
-
- [Função 2º grau] Dificuldade em resolver questões do tipo
por Richard Oliveira » Seg Nov 07, 2011 16:17
- 5 Respostas
- 3376 Exibições
- Última mensagem por Richard Oliveira

Seg Nov 07, 2011 21:05
Funções
-
- questoes de esfera
por camilalindynha » Ter Dez 11, 2007 09:12
- 1 Respostas
- 11223 Exibições
- Última mensagem por admin

Ter Dez 11, 2007 12:26
Geometria Espacial
-
- Questões da UFRGS
por Neperiano » Qua Fev 11, 2009 18:32
- 3 Respostas
- 24243 Exibições
- Última mensagem por rcompany

Qui Fev 21, 2019 23:21
Desafios Enviados
-
- resolução de questões
por emerson meneses » Ter Jul 07, 2009 17:28
- 0 Respostas
- 2253 Exibições
- Última mensagem por emerson meneses

Ter Jul 07, 2009 17:28
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


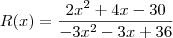
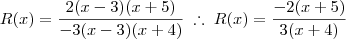
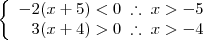
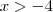 .
.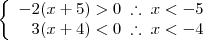
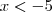 .
. 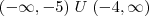
![fog(x) = f[g(x)] fog(x) = f[g(x)]](/latexrender/pictures/5fc1a848713041c51f0b0b0bf901805f.png)
![fog(\sqrt{2}) = f[g(\sqrt{2})] fog(\sqrt{2}) = f[g(\sqrt{2})]](/latexrender/pictures/33221b6d2ac008f45bb1b3cf5aff0ab7.png)
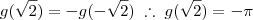
![fog(\sqrt{2}) = f[g(\sqrt{2})] = f(-\pi) = \sqrt{2} fog(\sqrt{2}) = f[g(\sqrt{2})] = f(-\pi) = \sqrt{2}](/latexrender/pictures/cd491170c94854e4e3e35879d512a096.png)

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
