 por Cleyson007 » Dom Mai 25, 2008 01:53
por Cleyson007 » Dom Mai 25, 2008 01:53
Boa noite Fábio Sousa, tudo bem?
Gostaria de saber se a resolução da questão abaixo está certa.
Um menino tem R$ 19,00 no seu cofre e, a partir de certo mês, passou a tirar R$ 0,80 todos os dias para um sorvete.
Pergunta-se: Qual foi o 1º dia em que ele não pôde tomar sorvete?
No meu modo de pensar o 1º dia em que ele não pode tomar sorvete foi quando acabou o dinheiro.
Se acabou o dinheiro eu coloquei 0 (zero) no termo geral da PA.
Resolvi a questão assim ----> 0 = 19 + (0,8n + 0,8), obtendo o valor de 24,75 para n.
O raciocício está correto?
Um abraço.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por admin » Dom Mai 25, 2008 02:45
por admin » Dom Mai 25, 2008 02:45
Olá Cleyson, tudo bem!
O menino não pôde comprar sorvete quando o saldo do cofre ficou inferior a 80 centavos!
Lembre-se que se

é o número de dias,
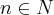
, ou seja,
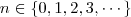
.
Veja o que aconteceu dia a dia com o saldo do cofre:
1º dia) saldo =
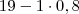
2º dia) saldo =

3º dia) saldo =


n-ésimo dia) saldo =

A pergunta é: quando o saldo ficou inferior a 80 centavos?
Ou seja, a partir de qual valor de

:

Resolva esta inequação, lembrando antes de responder que

é um número natural.
Para conferir, pense no caso real, testando o valor encontrado.
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Cleyson007 » Dom Mai 25, 2008 03:03
por Cleyson007 » Dom Mai 25, 2008 03:03
fabiosousa escreveu:Olá Cleyson, tudo bem!
O menino não pôde comprar sorvete quando o saldo do cofre ficou inferior a 80 centavos!
Lembre-se que se

é o número de dias,
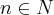
, ou seja,
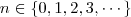
.
Veja o que aconteceu dia a dia com o saldo do cofre:
1º dia) saldo =
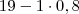
2º dia) saldo =

3º dia) saldo =


n-ésimo dia) saldo =

A pergunta é: quando o saldo ficou inferior a 80 centavos?
Ou seja, a partir de qual valor de

:

Resolva esta inequação, lembrando antes de responder que

é um número natural.
Para conferir, pense no caso real, testando o valor encontrado.
A resolução do sistema ficaria assim ----> 19 - 0,8 n < 0,8 0,8 - 19 < - 0,8 n - 18,2 < - 0,8 n ( -1)
Encontrando o valor de n > 22,75.
Observando que n é um nº real, a resposta seria n = 23 ? Pensando no caso real ---> 19 - 0,8 n < 0,8 para n = 23 19 - 0,8 (23) < 0,8 0,6 < 0,8 ( verdadeiro )
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por admin » Dom Mai 25, 2008 04:31
por admin » Dom Mai 25, 2008 04:31
Cleyson007 escreveu:A resolução do sistema ficaria assim ---->
19 - 0,8 n < 0,8

Encontrando o valor de n > 22,75.
Observando que n é um nº real, a resposta seria n = 23 ?
Cleyson,

é um número
natural,

.
De fato,
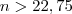
, mas cuidado na resolução da
inequação, não "sistema":

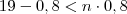



ou
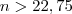
Portando, a partir de

(o 23º dia) o menino não pôde comprar sorvete, pois neste dia o saldo do cofre era de 60 centavos!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problema sobre Circunferência
 por Cleyson007 » Dom Jun 29, 2008 01:18
por Cleyson007 » Dom Jun 29, 2008 01:18
- 4 Respostas
- 7299 Exibições
- Última mensagem por Cleyson007

Dom Ago 24, 2008 17:25
Geometria Plana
-
- Problema sobre Conjuntos.
 por Vinicius » Dom Abr 05, 2009 17:12
por Vinicius » Dom Abr 05, 2009 17:12
- 4 Respostas
- 4510 Exibições
- Última mensagem por Vinicius

Dom Abr 05, 2009 22:17
Conjuntos
-
- Problema sobre Vetores
por Matphe1974 » Ter Jun 18, 2013 17:37
- 0 Respostas
- 1311 Exibições
- Última mensagem por Matphe1974

Ter Jun 18, 2013 17:37
Álgebra Linear
-
- Problema Sobre Diagrama de Venn
por PlasticHobo » Ter Out 04, 2011 19:54
- 1 Respostas
- 1925 Exibições
- Última mensagem por Neperiano

Qui Out 06, 2011 15:14
Estatística
-
- Problema sobre renda per capita
por matem » Dom Dez 11, 2011 09:01
- 3 Respostas
- 3754 Exibições
- Última mensagem por Neperiano

Dom Dez 11, 2011 13:07
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 é o número de dias,
é o número de dias, 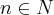 , ou seja,
, ou seja, 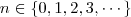 .
.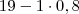







 .
.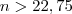 , mas cuidado na resolução da
, mas cuidado na resolução da 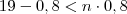



 (o 23º dia) o menino não pôde comprar sorvete, pois neste dia o saldo do cofre era de 60 centavos!
(o 23º dia) o menino não pôde comprar sorvete, pois neste dia o saldo do cofre era de 60 centavos!



 ,
,  ,
,  .
.

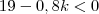
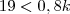


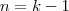
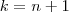


 dias, como já havíamos concluído.
dias, como já havíamos concluído.