Lucio Martins escreveu:A sombra de uma pessoa que tem 1,80m de altura esta medindo 60 cm. No mesmo momento, a seu lado, a sombra de um poste mede 2 m. Se , algum tempo depois , a sombra do poste diminui 50 cm, a sombra da pessoa passou a medir quantos:
Boa noite.
Vou te passar como eu faria e você tenta fazer (usando meu método ou pensando de alguma forma que você entenda melhor):
Isso nada mais é do que uma simples razão.
Se você pegar a altura da pessoa e dividir pelo tamanho da sombra da pessoa é igual a pegar o tamanho do poste e dividir pelo tamanho da sombra do poste. Perceba que o tamanho do poste nós não temos, então temos que achar ele inicialmente. Matematicamente falando, ficaria:
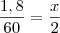
Multiplicando cruzado você descobre o valor de x. Mas não é isso que o problema quer. Você terá que montar uma nova razão, só que desta ver ao invés de usar 2 como tamanho da sombra, usará 1,5 e ao invés do 60, usará
y, pois é o que queremos descobrir (tamanho da sombra da pessoa agora).
Qualquer dúvida informe




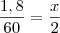




 , avisa que eu resolvo.
, avisa que eu resolvo.

