 por Mr Bob Wilson » Qua Mai 05, 2010 20:23
por Mr Bob Wilson » Qua Mai 05, 2010 20:23
Bom Dia ajudamatematica , estou com duvida nas relaçoes metricas no triangulo retangulo , eu tentei muitas e muitas vezes
mas não conseguir resolver certos exercicios , poderia me ajudar ?
1 - uma estaçao de tratamento de agua (ETA) localiza-se a 600 m de uma estrada reta . Uma estaçao de radio localiza-se nessa mesma estrada , a 1000 m da ETA . Pretende-se construir um restaurante , na estrada , que fique a mesma distancia das duas estaçoes . A distancia do restaurante a cada uma das estaçoes devera ser ?
2 - A diagonal de uma tela retangular de TV mede 22 polegadas . Quais sao as dimensoes da tela , tambem em polegadas , sabendo que a razao entre elas é 3/4 ?
3 - Uma escada de 25 dm de comprimento se apoia num muro do qual seu pé dista 7 dm . Se o pé da escada se afasta mais 8 dm dp ,irp . qiaç p desçpca,emtp verofocadp éça extre,odade siéropr da escada ?
ficarei grato , vlw
-
Mr Bob Wilson
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Mai 05, 2010 20:15
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Qua Mai 05, 2010 20:51
por Molina » Qua Mai 05, 2010 20:51
Boa noite.
O 1. você pode encontrar aqui:
viewtopic.php?f=81&t=969&p=3273&hilit=+ETA+#p3273Tente fazer o 2. e o 3. usando este exercício.
Qualquer dúvida, infome

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Mr Bob Wilson » Qua Mai 05, 2010 21:32
por Mr Bob Wilson » Qua Mai 05, 2010 21:32
Obrigado pelo atendimento molina
consegui entender a resoluçao do exercicio , mas eu não consegui enxergar o teorema de pitagoras nas outras
poderia me ajudar a fazer os outros ? tenho muita dificuldade nessa materia , vlw ^^
-
Mr Bob Wilson
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Mai 05, 2010 20:15
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Qua Mai 05, 2010 23:32
por Molina » Qua Mai 05, 2010 23:32
Boa noite, novamente.
Mr Bob Wilson escreveu:2 - A diagonal de uma tela retangular de TV mede 22 polegadas . Quais sao as dimensoes da tela , tambem em polegadas , sabendo que a razao entre elas é 3/4 ?
Você consegue visualizar uma TV com 22 polegadas de diagonal? Só que a
base dela (parte de baixo) é do tipo
4x polegadas e a
altura dela (lateral) é do tipo
3x polegadas.
Essa figura forma um triângulo retângulo, com catetos 3x e 4x, e hipotenusa 22.
Usando o Pit.:

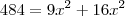

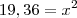
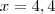
Jogando esse valor de x em
3x (altura) e
4x (base) você descobre as dimensões da tela.
Para verificar se seu valor é o correto, pegue esses valores da altura e da base, eleve elas ao quadrado e depois some. Tire a raiz quadrada desse total e verifique se deu 22 (medida da diagonal e hipotenusa).
Abraços,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Relações métricas num triângulo retângulo
por Marcampucio » Dom Abr 26, 2009 20:21
- 2 Respostas
- 7744 Exibições
- Última mensagem por Marcampucio

Ter Jun 02, 2009 13:41
Tópicos sem Interação (leia as regras)
-
- relaçoes metricas no triangulo retangulo
 por stanley tiago » Dom Jan 23, 2011 18:07
por stanley tiago » Dom Jan 23, 2011 18:07
- 2 Respostas
- 2288 Exibições
- Última mensagem por stanley tiago

Dom Jan 23, 2011 22:06
Geometria Plana
-
- [Relações métricas no triângulo Retângulo]
 por Gustavo Gomes » Sex Out 26, 2012 21:47
por Gustavo Gomes » Sex Out 26, 2012 21:47
- 1 Respostas
- 2230 Exibições
- Última mensagem por young_jedi

Sex Out 26, 2012 22:08
Geometria Plana
-
- Relações métricas no triângulo retângulo
 por Pandaludo » Qua Ago 07, 2013 21:32
por Pandaludo » Qua Ago 07, 2013 21:32
- 0 Respostas
- 1059 Exibições
- Última mensagem por Pandaludo

Qua Ago 07, 2013 21:32
Geometria Plana
-
- Relações métricas do triângulo , tangente à uma circunferênc
por c_zaidan » Sex Out 22, 2010 15:57
- 2 Respostas
- 2195 Exibições
- Última mensagem por c_zaidan

Sex Out 22, 2010 18:50
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





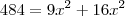

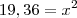
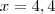


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.