por manuoliveira » Dom Mai 02, 2010 14:53
Sabendo-se que:
a² - b² = (a + b)(a - b)
a² + 2ab + b² = (a + b)²
a³ + b³ = (a + b)(a² - ab + b²)
sen(2x) = 2.(senx)(cosx)
cos(2x) = cos²x - sen²x
Encontre o valor de 16.(cos^6 15º + sen^6 15º)
Resposta: 13
-
manuoliveira
- Usuário Parceiro
-
- Mensagens: 61
- Registrado em: Qui Abr 01, 2010 19:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: cursando
por Molina » Dom Mai 02, 2010 16:04
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-
Molina
- Colaborador Moderador - Professor
-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
por manuoliveira » Dom Mai 02, 2010 19:41
obrigada!!
-
manuoliveira
- Usuário Parceiro
-
- Mensagens: 61
- Registrado em: Qui Abr 01, 2010 19:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: cursando
por Molina » Dom Mai 02, 2010 19:43
manuoliveira escreveu:obrigada!!
De nada!
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-
Molina
- Colaborador Moderador - Professor
-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problema Produtos Notáveis e Fatoração
por Diana » Qua Ago 17, 2011 22:08
- 1 Respostas
- 1823 Exibições
- Última mensagem por Caradoc
Qua Ago 17, 2011 23:12
Sistemas de Equações
-
- Produtos Notáveis
por Du21 » Ter Mar 29, 2011 20:31
- 2 Respostas
- 2348 Exibições
- Última mensagem por Du21
Ter Mar 29, 2011 21:02
Álgebra Elementar
-
- Produtos Notáveis
por Pri Ferreira » Qua Mai 23, 2012 00:10
- 0 Respostas
- 1110 Exibições
- Última mensagem por Pri Ferreira
Qua Mai 23, 2012 00:10
Álgebra Elementar
-
- Produtos Notáveis - dúvida
por laura_biscaro » Ter Fev 26, 2013 11:58
- 5 Respostas
- 2512 Exibições
- Última mensagem por e8group
Ter Fev 26, 2013 21:51
Álgebra Linear
-
- (algebra)Produtos notáveis
por Man Utd » Seg Abr 15, 2013 20:42
- 7 Respostas
- 3503 Exibições
- Última mensagem por DanielFerreira
Ter Abr 16, 2013 16:58
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
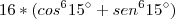
![16*[(cos^2 15\°)^2 + (sen^2 15\°)^3]](/latexrender/pictures/1ab7a176e7991ed7e3716a07c21046d2.png "16*[(cos^2 15\°)^2 + (sen^2 15\°)^3]")
![16*[(cos^2 15\°) + (sen^2 15\°)]*[cos^4 15\° - cos^2 15\°*sen^2 15\° + sen^4 15\°]](/latexrender/pictures/e73b1bfe1196fbbabefbf70d8973783f.png "16*[(cos^2 15\°) + (sen^2 15\°)]*[cos^4 15\° - cos^2 15\°*sen^2 15\° + sen^4 15\°]")
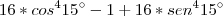
![16*1*[cos^4 15\° - \frac{1}{16} + sen^4 15\°]](/latexrender/pictures/3b742b531ca91a8cf792371e9a0c4e8f.png "16*1*[cos^4 15\° - \frac{1}{16} + sen^4 15\°]")
![16*[cos^4 15\° + sen^4 15\°] - 1](/latexrender/pictures/115e2e6a7913e188c45dbaa511725084.png "16*[cos^4 15\° + sen^4 15\°] - 1")
![16*[(cos^2 15\°)^2 + (sen^2 15\°)^2] - 1](/latexrender/pictures/18820446c4838815019f6f3938a27cfb.png "16*[(cos^2 15\°)^2 + (sen^2 15\°)^2] - 1")
![16*[(cos^2 15\° +sen^2 15\°)^2 - 2*(cos 15\° * sen 15\°)*(cos 15\° * sen 15\°)] - 1](/latexrender/pictures/2224c79bcb207340322c824bfc305b89.png "16*[(cos^2 15\° +sen^2 15\°)^2 - 2*(cos 15\° * sen 15\°)*(cos 15\° * sen 15\°)] - 1")
![16*[1 - sen 30 \° * \frac{sen 30 \°}{2}] - 1](/latexrender/pictures/b8d6378ee3613abe4cc0c52c929e1f04.png "16*[1 - sen 30 \° * \frac{sen 30 \°}{2}] - 1")
![16*[1 - \frac{1}{2}*\frac{1}{4}] - 1](/latexrender/pictures/04962867f8b389edd75b022c48f401e8.png "16*[1 - \frac{1}{2}*\frac{1}{4}] - 1")
