 por studieren » Sáb Mai 01, 2010 17:39
por studieren » Sáb Mai 01, 2010 17:39
Qual o menor valor com x real de

?
Tentei resolver, mas não consegui. O resultado será dado em graus ou com o valor de -1, pois cos 180 admite este valor mínimo. Seria então
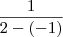
?
-
studieren
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Jan 01, 2010 22:34
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Neperiano » Sáb Mai 01, 2010 19:05
por Neperiano » Sáb Mai 01, 2010 19:05
Ola
Substituindo x por 1
Ficaria o que voce escreveu entretanto cos 1 é positivo, feito isso some embaixo e depois divida, o resultado sera 1
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por MarceloFantini » Dom Mai 02, 2010 14:59
por MarceloFantini » Dom Mai 02, 2010 14:59
Substituindo x por 1 você tem
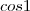
que é aproximadamente
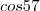
, que ninguém sabe o valor. O valor mínimo da expressão será quando o denominador for máximo, então a sua resposta está certa studieren, só que de maneira mais geral será:
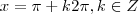
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Neperiano » Dom Mai 02, 2010 15:10
por Neperiano » Dom Mai 02, 2010 15:10
Ola
Desculpe mas agora eu não entendi, cos 1 = cos 57 com assim?
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por MarceloFantini » Seg Mai 03, 2010 17:12
por MarceloFantini » Seg Mai 03, 2010 17:12
Cosseno de 1 radiano é aproximadamente cosseno de 57 graus.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Neperiano » Seg Mai 03, 2010 17:37
por Neperiano » Seg Mai 03, 2010 17:37
Ah tah tu ta falando de conversão de radiano para graus
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por studieren » Qua Mai 05, 2010 04:05
por studieren » Qua Mai 05, 2010 04:05
Valeu !
-
studieren
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Jan 01, 2010 22:34
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Valor mínimo
 por FilipeCaceres » Qui Mai 26, 2011 19:53
por FilipeCaceres » Qui Mai 26, 2011 19:53
- 13 Respostas
- 8435 Exibições
- Última mensagem por demolot

Sex Mai 27, 2011 19:31
Funções
-
- Valor mínimo da função
por maria cleide » Seg Out 24, 2011 20:00
- 0 Respostas
- 845 Exibições
- Última mensagem por maria cleide

Seg Out 24, 2011 20:00
Funções
-
- Função real de variável real!
por kellykcl » Qui Mai 01, 2014 13:41
- 2 Respostas
- 3267 Exibições
- Última mensagem por kellykcl

Qui Mai 01, 2014 16:28
Funções
-
- [Valor de Mercadoria] A partir do valor total de venda
por Gerson Belini » Qua Out 02, 2013 02:17
- 0 Respostas
- 3902 Exibições
- Última mensagem por Gerson Belini

Qua Out 02, 2013 02:17
Matemática Financeira
-
- [Calcule o valor de Seno de 18º] Expressar o valor numérico
por VictorFPS » Sáb Fev 14, 2015 20:01
- 1 Respostas
- 3863 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:41
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 ?
? ?
?
 ?
? ?
?

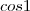 que é aproximadamente
que é aproximadamente 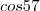 , que ninguém sabe o valor. O valor mínimo da expressão será quando o denominador for máximo, então a sua resposta está certa studieren, só que de maneira mais geral será:
, que ninguém sabe o valor. O valor mínimo da expressão será quando o denominador for máximo, então a sua resposta está certa studieren, só que de maneira mais geral será: 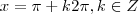 .
.







 .
.



