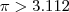por Questioner » Ter Abr 20, 2010 22:20
por Questioner » Ter Abr 20, 2010 22:20
Olá!Há algum tempo eu, durante um exercício, provei que
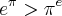
Infelizmente, não consigo provar novamente. Alguém pode me dar uma luz? Não me lembro nem por onde começar...
Agradeço desde já!Abraços.

-
Questioner
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Abr 20, 2010 22:13
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Elcioschin » Qua Abr 21, 2010 22:06
por Elcioschin » Qua Abr 21, 2010 22:06
pi^e ~= 22,459
e^pi ~= 23,140
Que outra prova você quer?
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Questioner » Sex Abr 23, 2010 19:26
por Questioner » Sex Abr 23, 2010 19:26
Por cálculo é possível se determinar que
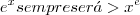
.
Quero saber como essa conclusão foi feita utilizando cálculo. Se eu quisesse só a resposta, uma calculadora bastaria, como você percebeu.
-
Questioner
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Abr 20, 2010 22:13
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Molina » Sex Abr 23, 2010 19:38
por Molina » Sex Abr 23, 2010 19:38
Questioner escreveu:Por cálculo é possível se determinar que
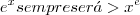
.
Quero saber como essa conclusão foi feita utilizando cálculo. Se eu quisesse só a resposta, uma calculadora bastaria, como você percebeu.
Boa noite.
Você consegue provar essa sua afirmação?
Acho que você poderia tirar o limite de ambos os lados, com x tendendo a

, assim:
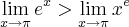
Será que é daqui pra frente?
Questão interessante...
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por MarceloFantini » Sáb Abr 24, 2010 01:13
por MarceloFantini » Sáb Abr 24, 2010 01:13
Agora a questão ficou mais forte, você não quer provar que vale apenas pra pi, mas para qualquer x. Não sei como ajudar, mas fui no wolframalpha dar uma checada e acho que não é para todo x, tem que estabelecer uma restrição.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Elcioschin » Sáb Abr 24, 2010 10:07
por Elcioschin » Sáb Abr 24, 2010 10:07
A curva de e^x é uma exponencial padrão.
A curva de x^e é similar à curva e^x e realmente fica sempre abaixo da primeira.
Eu não conheço a demonstração de que e^x > x^e, mas acredito que ela exista.
Partindo do princípio de que a demonstração existe, ela é deve ser válida para qualquer valor de x, logo deve valer para x = pi, isto é, e^pi > pi^e.
Suponho que a prova deve partir de
Limite (1 + 1/x)^x = e
x-->oo
Limite [(1 + 1/x)^x]^x = e^x -----> Limite (1 + 1/x)^x² = e^x
x-->oo .................................x-->oo
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Questioner » Sáb Abr 24, 2010 12:18
por Questioner » Sáb Abr 24, 2010 12:18
-
Questioner
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Abr 20, 2010 22:13
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Questioner » Sáb Abr 24, 2010 12:42
por Questioner » Sáb Abr 24, 2010 12:42
Acho que encontrei a resposta. Vejam se confere, por favor:
Temos que considerar que:
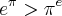
somente se

, sendo assim:
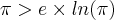
Isso só será verdade se:
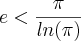
Isso nos leva a
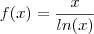
Isso, numericamente, confere.
Ou mesmo se fizermos ao contrário:
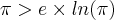
e substituirmos numericamente, encontraremos que
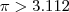
Será que é isso?
-
Questioner
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Abr 20, 2010 22:13
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limite e neperiano
por Zkz » Sáb Set 13, 2008 20:30
- 1 Respostas
- 5534 Exibições
- Última mensagem por admin

Ter Set 16, 2008 21:20
Cálculo: Limites, Derivadas e Integrais
-
- Exponencial neperiano envolvendo complexos
por marciopc » Sáb Out 31, 2009 12:56
- 0 Respostas
- 1964 Exibições
- Última mensagem por marciopc

Sáb Out 31, 2009 12:56
Funções
-
- Derivadas parciais com neperiano e seno.
por iksin » Qui Set 20, 2018 14:20
- 1 Respostas
- 5654 Exibições
- Última mensagem por Gebe

Qui Set 20, 2018 14:39
Cálculo: Limites, Derivadas e Integrais
-
- Problema sobre PA
por Cleyson007 » Dom Mai 25, 2008 01:53
- 3 Respostas
- 7998 Exibições
- Última mensagem por admin

Dom Mai 25, 2008 04:31
Progressões
-
- Dúvida sobre PA
por Cleyson007 » Ter Mai 27, 2008 23:22
- 3 Respostas
- 5002 Exibições
- Última mensagem por admin

Sáb Mai 31, 2008 21:57
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
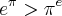

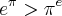


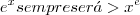 .
.
.
 , assim:
, assim: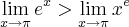





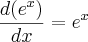
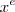
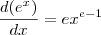

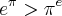 somente se
somente se  , sendo assim:
, sendo assim: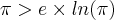
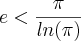
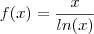
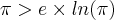 e substituirmos numericamente, encontraremos que
e substituirmos numericamente, encontraremos que