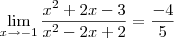Tenho, por exemplo, o limite abaixo:
Lim

x->-1
Se eu substituir -1 no denominador vou obter 0, então pelo método de Briot Rufini tento retirar a indeterminação, mas minha professora explicou que o último número deve zerar porém não é o que acontece:
-> primeiro repito o primeiro número para baixar o grau, depois multiplico 1 por -1 e somo com o -1 do x², que fica -2, depois o multiplico por -1 e somo com 2, o que vai resultar em 4, e não em zero como deveria ser!
x²-2x+4
Eu estou calculando errado ou último número pode ser qualquer número? O método do Rufini serve para baixar o grau de qualquer expressão?
Obrigada



 . e resultou que:
. e resultou que:




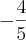
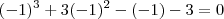

 ,
,  ,
,  , etc. (sem esquecer das potências de
, etc. (sem esquecer das potências de 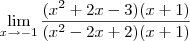 =
=