Comissão de 3

[estudandoMat]

Se temos um numero de alunos em um curso:
Noturno:
homens = 2
mulheres = 4
Diurno:
homens = 5
mulheres = 9

Três alunos do curso são escolhidos ao acaso para formarem a comissão de formatura. A
probabilidade de que a comissão seja composta por duas pessoas do noturno e uma do diurno é de:

Resposta: 7/38
----------------------------
Resolvendo:
Montei assim:
probabilidade de 6 de 20 , depois 5 de 19 , 14 (diurno) de 18 possiveis.
=

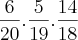Mas esta errado e n consigo encontrar o erro.

[MarceloFantini]

Não vejo erro nos seus cálculos e nem no raciocínio. É possível que o gabarito esteja errado.

[rassis46]

A resposta 7/38 está correcta e confirmada por simulação de Monte-Carlo.

[estudandoMat]

e como seria?

[rassis46]

Correcção:

Utilizando simulação de Monte Carlo:

A resposta 0,18421 está correcta se houver (teoricamente) reposição da amostra - o que não se coaduna com o enunciado do caso.
A resposta 6/20 x 5/19 x 14/18 = 0,0614 (ou por qualquer outra ordem) está correcta se não houver reposição da amostra - o que está desta vez de acordo com o enunciado.

A minha anterior afirmação foi precipitada. Peço desculpa.

[Lucio Carvalho]

Olá estudandoMat,
Concordo com a resposta 7/38.
Na contagem dos casos favoráveis e casos possíveis temos que usar "Combinações" e não "Arranjos sem repetição" porque na formação das comissões a ordem não interessa, isto é, falar "José, Maria e Pedro " é o mesmo que falar "Maria, Pedro e José. Assim,



Espero ter ajudado!