 por estudandoMat » Qui Abr 08, 2010 17:15
por estudandoMat » Qui Abr 08, 2010 17:15
Se temos um numero de alunos em um curso:
Noturno:
homens = 2
mulheres = 4
Diurno:
homens = 5
mulheres = 9
Três alunos do curso são escolhidos ao acaso para formarem a comissão de formatura. A
probabilidade de que a comissão seja composta por duas pessoas do noturno e uma do diurno é de:
Resposta: 7/38
----------------------------
Resolvendo:
Montei assim:
probabilidade de 6 de 20 , depois 5 de 19 , 14 (diurno) de 18 possiveis.
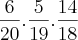
=

Mas esta errado e n consigo encontrar o erro.
-
estudandoMat
- Usuário Parceiro

-
- Mensagens: 52
- Registrado em: Sex Abr 02, 2010 00:29
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por MarceloFantini » Qui Abr 08, 2010 20:00
por MarceloFantini » Qui Abr 08, 2010 20:00
Não vejo erro nos seus cálculos e nem no raciocínio. É possível que o gabarito esteja errado.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por rassis46 » Sex Abr 16, 2010 11:34
por rassis46 » Sex Abr 16, 2010 11:34
A resposta 7/38 está correcta e confirmada por simulação de Monte-Carlo.
-
rassis46
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qui Abr 15, 2010 19:35
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Doutoramento em Engenharia mecânica
- Andamento: formado
 por estudandoMat » Sex Abr 16, 2010 14:06
por estudandoMat » Sex Abr 16, 2010 14:06
e como seria?
-
estudandoMat
- Usuário Parceiro

-
- Mensagens: 52
- Registrado em: Sex Abr 02, 2010 00:29
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por rassis46 » Sáb Abr 17, 2010 22:11
por rassis46 » Sáb Abr 17, 2010 22:11
Correcção:
Utilizando simulação de Monte Carlo:
A resposta 0,18421 está correcta se houver (teoricamente) reposição da amostra - o que não se coaduna com o enunciado do caso.
A resposta 6/20 x 5/19 x 14/18 = 0,0614 (ou por qualquer outra ordem) está correcta se não houver reposição da amostra - o que está desta vez de acordo com o enunciado.
A minha anterior afirmação foi precipitada. Peço desculpa.
-
rassis46
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qui Abr 15, 2010 19:35
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Doutoramento em Engenharia mecânica
- Andamento: formado
 por Lucio Carvalho » Sáb Abr 17, 2010 23:20
por Lucio Carvalho » Sáb Abr 17, 2010 23:20
Olá estudandoMat,
Concordo com a resposta 7/38.
Na contagem dos casos favoráveis e casos possíveis temos que usar "Combinações" e não "Arranjos sem repetição" porque na formação das comissões a ordem não interessa, isto é, falar "José, Maria e Pedro " é o mesmo que falar "Maria, Pedro e José. Assim,

Espero ter ajudado!
-

Lucio Carvalho
- Colaborador Voluntário

-
- Mensagens: 127
- Registrado em: Qua Ago 19, 2009 11:33
- Localização: Rua 3 de Fevereiro - São Tomé
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Física/Química
- Andamento: formado
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
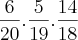 =
= 







 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
