Grafico de limites e assintotas

[Bruhh]

Olá, Boa Tarde!
Tenho a seguinte função para montar o gráfico e determinar as assíntotas horizontal e vertical:


f(x)=
|x|, se
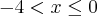
4, se
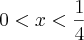
2, se
, se


Então, como é que eu monto o gráfico dessa função??
Eu sei que para calcular a assíntota horizontal, x deve tender infinito ou infinito negativo, mas onde eu calculo isso?
Também sei que para calcular a assíntota vertical, x deve tender a um número que zere o denominador, no caso de uma fração.
Mas eu não sei nem por onde começo, como monto o gráfico ou como calculo as assíntotas.Alguém, por favor ,poderia me ajudar?
-
Obrigada desde já!

[MarceloFantini]

Ainda não tentei resolver a questão mas lembre-se da definição de assíntota: é a reta que representa o valor que a função se aproxima cada vez mais, sem nunca assumir. Talvez ajude. Tente plotar o gráfico também, não parece difícil, e ter alguma dica geométrica.

[Bruhh]

Eu já li e reli várias vezes a função mas não consigo entender.
Como eu faço para saber onde esta a assíntota se não existem contas, só valores?Como vou calcular essas assíntotas??

Por favor, me ajuda, é muitooooooooo importante!

Obrigada

[Marcampucio]

Essa função é composta por vários segmentos de retas. Não tem assintotas.