 por cristina » Qui Abr 15, 2010 09:33
por cristina » Qui Abr 15, 2010 09:33
Bom dia estou precisando de uma ajuda...
tenho um problema: Sendo a a medida do apótema de um hexágono regular, a area desse hexagono vale:
![3{a}^{2} \sqrt[]{3} 3{a}^{2} \sqrt[]{3}](/latexrender/pictures/b9b10dfbf9b64cdced8eab89017ea81f.png)
![2{a}^{2} \sqrt[]{3} 2{a}^{2} \sqrt[]{3}](/latexrender/pictures/06707abfc19553f8b4d36bec1d507cef.png)
![3{a}^{2} \sqrt[]{2} 3{a}^{2} \sqrt[]{2}](/latexrender/pictures/33267ebc6f09a7466250d33fd31d5182.png)
![2{a}^{2} \sqrt[]{2} 2{a}^{2} \sqrt[]{2}](/latexrender/pictures/e9025e8cd9f15bc0b236a4a9230784bd.png)
Essas são as alternativas possiveis, mas nos exemplos que consigo nos livros geralmente vem em fração, por favor se alguem puder me ajudar agradeço....
-
cristina
- Usuário Parceiro

-
- Mensagens: 82
- Registrado em: Qua Set 02, 2009 17:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura/ matematica
- Andamento: cursando
 por Douglasm » Qui Abr 15, 2010 09:52
por Douglasm » Qui Abr 15, 2010 09:52
Ao desenharmos um hexágono, podemos dividí-lo em 6 triângulos com vértices no centro do polígono. Sendo um hexágono regular, todos os triângulos são equiláteros (só para garantir, observe que se dividirmos o ângulo de 360º no centro pelos 6 triângulos, veremos que cada um possui um ângulo de 60º, como o hexágono é regular eles também são isósceles, nos dizendo então que eles são todos equiláteros.). Deste modo, sendo o apótema igual a
a e considerando
x igual ao lado do triângulo, temos:

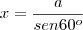
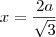

Já temos então o lado do hexágono (assim como dos triângulos equiláteros que o formam) e a altura (apótema). Agora é só observar que a área
S do hexágono é também a área dos 6 triângulos:

(ou de outro modo, podemos dizer que:

, onde
p é o semiperímetro)
Só falta substituir:

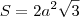
Até a próxima.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por cristina » Qui Abr 15, 2010 15:35
por cristina » Qui Abr 15, 2010 15:35
Obrigada Douglas, agora consegui entender, sua explicação foi bem facil de entender, mais uma
vez obrigada pela sua ajuda...
Até a proxima
-
cristina
- Usuário Parceiro

-
- Mensagens: 82
- Registrado em: Qua Set 02, 2009 17:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura/ matematica
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![3{a}^{2} \sqrt[]{3} 3{a}^{2} \sqrt[]{3}](/latexrender/pictures/b9b10dfbf9b64cdced8eab89017ea81f.png)
![2{a}^{2} \sqrt[]{3} 2{a}^{2} \sqrt[]{3}](/latexrender/pictures/06707abfc19553f8b4d36bec1d507cef.png)
![3{a}^{2} \sqrt[]{2} 3{a}^{2} \sqrt[]{2}](/latexrender/pictures/33267ebc6f09a7466250d33fd31d5182.png)
![2{a}^{2} \sqrt[]{2} 2{a}^{2} \sqrt[]{2}](/latexrender/pictures/e9025e8cd9f15bc0b236a4a9230784bd.png)



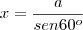
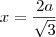

 (ou de outro modo, podemos dizer que:
(ou de outro modo, podemos dizer que:  , onde
, onde 
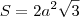

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.