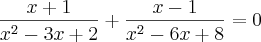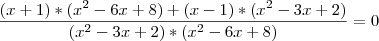por CaAtr » Qui Abr 08, 2010 17:46
por CaAtr » Qui Abr 08, 2010 17:46
Resolva em R:
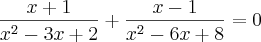
Resposta : s =
![\left[\frac{-1}{2},3 \right] \left[\frac{-1}{2},3 \right]](/latexrender/pictures/47e9d79adbb41d4aad249057b592080c.png)
Poderiam me dar uma dica..eu tirei mmc e ficou assim:

, mas nem sei se esta certo!
Desde de ja obrigada!!
-
CaAtr
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Ter Mar 09, 2010 20:04
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Qui Abr 08, 2010 17:59
por Molina » Qui Abr 08, 2010 17:59
CaAtr escreveu:Resolva em R:
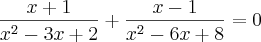
Resposta : s =
![\left[\frac{-1}{2},3 \right] \left[\frac{-1}{2},3 \right]](/latexrender/pictures/47e9d79adbb41d4aad249057b592080c.png)
Poderiam me dar uma dica..eu tirei mmc e ficou assim:

, mas nem sei se esta certo!
Desde de ja obrigada!!
Boa tarde.
Você tem a opção de passar uma das frações por outro lado e multiplicar cruzado, evitando assim o mmc. Caso queira fazer o mmc eu fiz multiplicando ambos os denominadores:
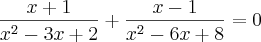
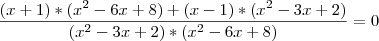



Agora é só achar as raízes.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por CaAtr » Sex Abr 09, 2010 15:54
por CaAtr » Sex Abr 09, 2010 15:54
Sim sim!! Obrigada!! Ja deu certo ja!!

-
CaAtr
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Ter Mar 09, 2010 20:04
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equações de 1 grau e 2 grau
por Neperiano » Sex Out 10, 2008 22:22
- 7 Respostas
- 13961 Exibições
- Última mensagem por DanielFerreira

Dom Jul 26, 2009 12:55
Desafios Médios
-
- problema de 1° grau
por heroncius » Sex Set 07, 2007 11:44
- 2 Respostas
- 5872 Exibições
- Última mensagem por heroncius

Sáb Set 08, 2007 20:52
Sistemas de Equações
-
- problema 1° grau
por heroncius » Dom Set 23, 2007 19:43
- 1 Respostas
- 2327 Exibições
- Última mensagem por admin

Seg Set 24, 2007 01:31
Equações
-
- Polinômio (grau 4)
por Cleyson007 » Ter Jun 02, 2009 15:36
- 2 Respostas
- 2908 Exibições
- Última mensagem por Cleyson007

Qua Jun 03, 2009 11:59
Polinômios
-
- Função do 2° Grau
por mimi2009 » Qua Jun 10, 2009 05:46
- 1 Respostas
- 2083 Exibições
- Última mensagem por Molina

Qua Jun 10, 2009 08:05
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
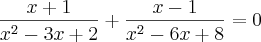
![\left[\frac{-1}{2},3 \right] \left[\frac{-1}{2},3 \right]](/latexrender/pictures/47e9d79adbb41d4aad249057b592080c.png)
 , mas nem sei se esta certo!
, mas nem sei se esta certo!
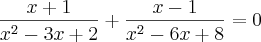
![\left[\frac{-1}{2},3 \right] \left[\frac{-1}{2},3 \right]](/latexrender/pictures/47e9d79adbb41d4aad249057b592080c.png)
 , mas nem sei se esta certo!
, mas nem sei se esta certo!
, mas nem sei se esta certo!